Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 9
Determine a resistência equivalente Rab para cada um dos circuitos da Figura P3.9.
Passo 1
Fala, galera! Beleza? Espero que sim. Hoje vamos resolver mais uma questão simples de circuito elétricos, vem comigo.
Abaixo temos os circuitos que serão analisados.
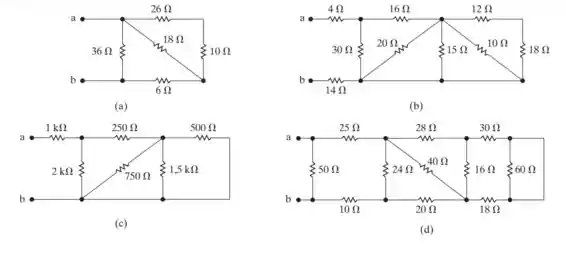
(a)
(b) Dada a complexidade maior da letra b, irei desenhar cada etapa:
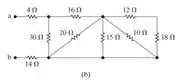
Após a operação em azul ficamos com 20||30 = 12 e agora basta somar 12+14+4 e obteremos a resistência equivalente.
Passo 2
(c) Na letra C o bizu é prestar atenção que temos resistências em , então, basta mudar tudo que for para .
Passo 3
(d) Bizu da questão: Note que o resistor de 60 está morto, pois ele está em curto, então, podemos simplesmente retirar ele do circuito. 
Do circuito resultante ficamos com 18+30 em paralelo com 16, e isso resulta em um resistor de 12.
Agora temos um resistor de 40 em paralelo com um de 40 (a soma do de 12 com o de 28) e com isso obtemos um de 20
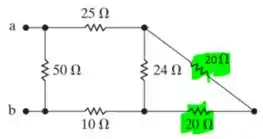
Nessa etapa temos um resistor de 40(soma dos 2 de 20) em paralelo com o de 24 e isso resulta em um resistor de 15
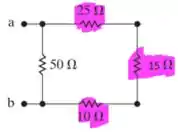
Por fim temos 50 em paralelo com 50 e obtemos
Resposta
(a) 12
(b) 30
(c) 1400
(d) 25