Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 60

Determine a resposta v R ( t ) para t > 0 no circuito da figura. Seja R = 3 Ω ,   L = 2 H   e   C = 1 8 F .

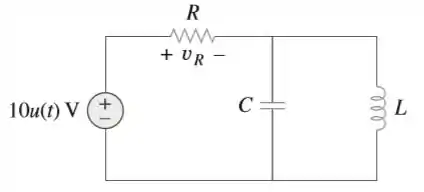
Passo 1

Desenhando o circuito no domínio de Laplace (domínio s), teremos:

Passo 2

A impedância total do circuito será:

Z ( s ) = 3 + ( 2 s / / 18 s ) = 3 s 2 + 18 s + 27 s 2 + 9

Passo 3

Temos então, o circuito mais simplificado para facilitar a visualização:

Passo 4

A corrente I ( s ) será encontrada com a primeira Lei de Ohm:

I ( s )   =   10 s Z ( s )

Substituindo o Z ( s ) podemos achar:

I ( s )   =   10 3 s ( s 2 + 9 s 2 + 6 s + 9 )

E a tensão V R ( s ) na figura do Passo 1 será:

V R ( s ) = 3 I ( s )

Substituindo I ( s ) teremos:

V R ( s ) = 10 s ( s 2 + 9 s 2 + 6 s + 9 )

Passo 5

Separando em frações parciais teremos:

V R ( s ) = 10 s ( s 2 + 9 s 2 + 6 s + 9 ) = A s + B s + C ( s + 3 ) 2

Agora basta encontrar A ,   B   e   C e encontrar V R ( s ) .

A = 10

B = 0

C =   - 60

Daí, substituindo, teremos:

V R ( s ) = 10 [ 1 s - 6 ( s + 3 ) 2 ]

Por Laplace utilizando a tabela de transformadas, teremos:

v R ( t )   = ( 10 - 60 t   e - 3 t ) u ( t )   V .

Resposta

v R ( t )   = ( 10 - 60 t   e - 3 t ) u ( t )   V .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Projete um circuito R L C ressonante em paralelo com ω 0 = 10 r a d s e Q = 20 . Calcule a largura de banda do circuito. Considere R = 10 Ω .
Refaça o Problema 14.25 para o caso no qual os elementos estejam ligados em paralelo.Problema 14.2514.25 Um circuito R L C em série tem R=2k Ω , L=40m H e C=1µ F µ . Calcule a impedância na ressonânci
Considere os circuitos da F i g u r a14.81 e determine a frequência de ressonância ω 0 , o fator de qualidade Q e a largura de banda B .
Calcule a frequência de ressonância de cada um dos circuitos da F i g u r a14.82
Considere os circuitos da F i g u r a14.81 e determine a frequência de ressonância ω 0 , o fator de qualidade Q e a largura de banda B .