Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 50
Determine que tipo de filtro é aquele da Figura . Calcule a frequência de corte .
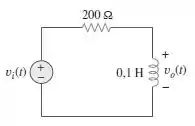
Passo 1
Vamos achar a função de transferência do circuito, pessoal!
Passo 2
Fazendo e , podemos determinar o tipo de filtro com o qual estamos lidando! Assim,
Como e , nós temos que esse circuito é de um filtro passa-alta.
Passo 3
Para encontrarmos a frequência de corte, nós colocamos igual a :
Assim,
Ou
Resposta
Temos um filtro passa-alta com frequência de corte;
Exercícios de Livros Relacionados
a) Determine a expressão numérica para a função de transferência H(s) = Vo/Vi para o circuito na Figura P13.51.b) Determine o valor numérico de cada polo e zero de H(s).
a) Determine a função de transferência Io/I g como uma função de μ , para o circuito da Figura P13.57. b) Determine o maior valor de m que produzirá um sinal de saída limitado para um sinal de entrada
Determine a expressão numérica para a função de transferência (Vo/Vi ) de cada circuito da Figura P13.52 e os valores numéricos dos polos e zeros de cada função de transferência. Determine a expressão
O amplificador operacional no circuito da Figura P13.53 é ideal. a) Determine a expressão numérica para a função de transferência H(s) = Vo/Vg. b) Determine o valor numérico de cada zero e polo de H(s