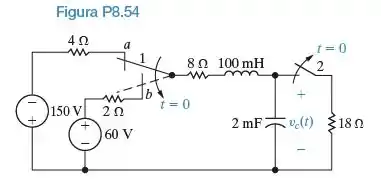
As duas chaves no circuito visto na Figura P8.54 funcionam de modo sincronizado. Quando a chave 1 está na posição a, a chave 2 está fechada. Quando a chave 1 está na posição b, a chave 2 está aberta. A chave 1 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b.

Determine vC(t) para .

Fala meu povo, tudo belezinha? Começando, temos que em

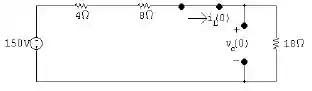
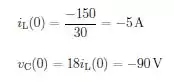
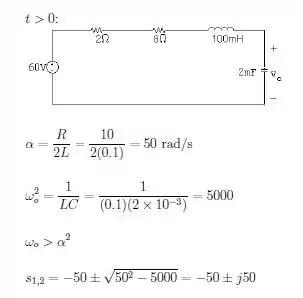
Para

Em outubro de 1745, Ewald Georg von Kleist, descobriu que uma carga poderia ser armazenada, conectando um gerador de alta tensão eletrostática por um fio a uma jarra de vidro com água, que estava em sua mão.[1] A mão de Von Kleist e a água agiram como condutores, e a jarra como um dielétrico (mas os detalhes do mecanismo não foram identificados corretamente no momento). Von Kleist descobriu, após a remoção do gerador, que ao tocar o fio, o resultado era um doloroso choque. Em uma carta descrevendo o experimento, ele disse: "Eu não levaria um segundo choque pelo reino de França".[2] No ano seguinte, na Universidade de Leiden, o físico holandês Pieter van Musschenbroek inventou um capacitor similar, que foi nomeado de Jarra de Leiden.[3]