A função na figura é movida da posição 1 para a 2 em . Determine para todo .
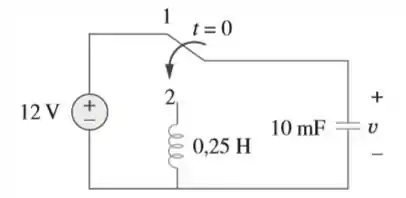
Passo 1
Vamos redesenhar o circuito da seguinte maneira para , o capacitor funciona como um circuito aberto!
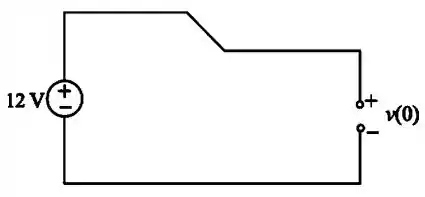
Passo 2
A partir dessa figura do Passo 1, concluímos que
Com isso, vamos redesenhar a figura para :
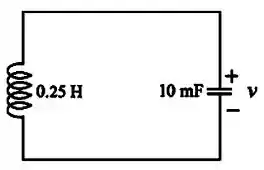
Passo 3
Agora, vamos redesenhar novamente o circuito do Passo 3, mas dessa vez no domínio de Laplace e incorporando a condição inicial do capacitor:
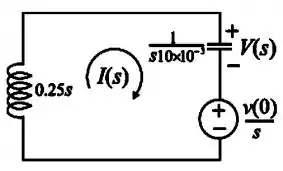
Passo 4
Agora podemos aplicar a lei de Kirchhoff das tensões e isolar o nosso
Passo 5
Daí, vamos escrever a expressão para a tensão que passa pelo capacitor em domínio de Laplace utilizando a primeira lei de Ohm:
Passo 6
Em seguida, vamos substituir onde for e em seguida separar em frações parciais:
Agora basta encontrar (utilizando o método dos resíduos) e encontrar .
Daí, substituindo, teremos:
Por Laplace utilizando a tabela de transformadas, teremos:
, para t>0
Resposta
, para t>0