Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 75
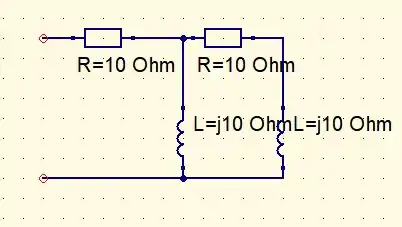
Projete um circuito que transforme uma entrada de tensão senoidal em uma saída de tensão cossenoidal.
Passo 1
Primeiro devemos lembrar da relação entre uma cossenoide e uma senóide que é dada por
Isso nos indica que nossa saída deve deslocar nossa entrada em . Para alcançar o resultado esperado podemos utilizar um circuito com valor (em módulo) dos resistores e indutores iguais e esse resultado já é bem padronizado e bastante utilizado. Assim, nosso circuito fica sendo o seguinte
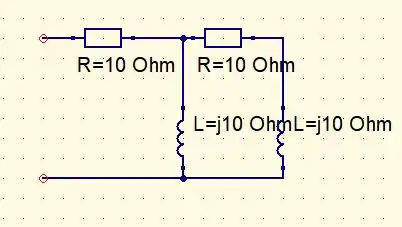
Onde a tensão de entrada é medida nos terminais da esquerda do circuito e a tensão de saída pela tensão no indutor mais a direita.
Resposta
Exercícios de Livros Relacionados
Converta as seguintes funçōes para funçōes coseno com amplitudes positivas:(a) 6 s e n 2 t + 15 ∘ , (b) - 2 c o s 4 t + 10 ∘ , (c) 8 c o s 5 t - 15 s e n 5 t .
Calcule i 4 , usando somente as propriedades das senóides se ( b ) i 1 = 5 c o s 3 t + 30 ∘ A , i 2 = 5 s e n 3 tA , e i 3 = 5 c o s 3 t + 150 ∘ A
Determinar se v 1 está adiantada ou atrasada em relaçáo a v 2 e de quanto.(b) v 1 = 10 c o s 4 t , v 2 = 5 c o s 4 t + 12 s e n 4 t ,
Determinar se v 1 está adiantada ou atrasada em relaçáo a v 2 e de quanto.(c) v 1 = 20 ( c o s 4 t + 83 s e n 4 t ) , v y = 3 c o s 4 t + 4 s e n 4 t .
Dada a tensão v = 100 c o s 400 π t + 45 ∘ V , calcule (a) sua amplitude, (b) seu ångulo de fase em graus, (c) seu ângulo de fase em radianos, (d) seu periodo em ms, (e) sua frequência em rad/s, (f)