Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 42
42- Uma fonte de é aplicada a uma impedância de carga . A potência aparente entrando na carga é de com um fator de potência atrasado.
Calcule a potência complexa
Determine a corrente fornecida para a carga
Determine
Supondo que , determine os valores de e
Passo 1
Lembre-se que quando diz que o fator de potência está atrasado é por que a reatância equivalente no sistema acaba por ser indutivo. Então nós teremos um ângulo de fase positivo e que será igual a:
E como temos uma potência aparente (ou total) igual a então teremos o seguinte triângulo de potências:
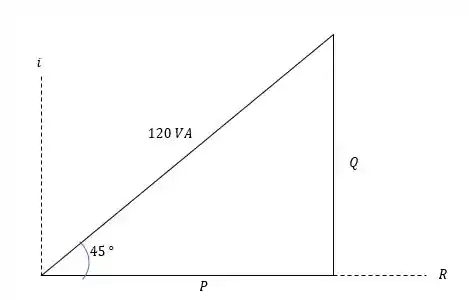
Então a potência complexa (ou potência total, só que escrita como um número complexo) será:
Essa medida nos diz que temos uma potência real de e uma potência reativa de
Passo 2
A potência complexa pode ser calculada da seguinte forma:
Porém como não estamos interessados no ângulo de fase dos componentes então vamos ignorar os ângulos por enquanto.
Logo a amplitude de será:
Mas adiantando, como a potência tem um fator de potência atrasado e a tensão não tem nenhum atraso então a corrente estará atrasado em da tensão.
Passo 3
E a impedância .
Sabendo que a impedância terá um ângulo de então:
Passo 4
Pelo valor que encontramos no passo anterior vemos que:
Ou seja: