Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 52

O resistor de 160 V no circuito da Figura P10.51 é substituído por uma impedância variável Zo. Admita que Zo seja ajustada para transferência de máxima potência média.

a) Qual é a máxima potência média fornecida a Zo?

b) Qual é a potência média fornecida pela fonte de tensão ideal, quando Zo absorve a máxima potência média?

c) Escolha componentes individuais do Apêndice H para formar uma impedância que dissipe a potência média mais próxima do valor do item (a). Assuma que a frequência da fonte é 60 Hz.

Passo 1

Beleza pessoal?! Espero que sim, pois agora iremos dar continuidade a mais uma questão com padrão responde ai de qualidade.

  1. Para darmos início, iremos desconectar a carga como mostrado na figura, assim nosso circuito terá apenas uma malha para equacionarmos.

    2. 5120 = 30 I 1 + j 100 I 1 + j 40 I 1 + j 64 I 1 + j 40 I 1           ( 1 )

    I 1 = 5120 30   +   j 244

    =   2.54   - j 20.67     A ( r m s )

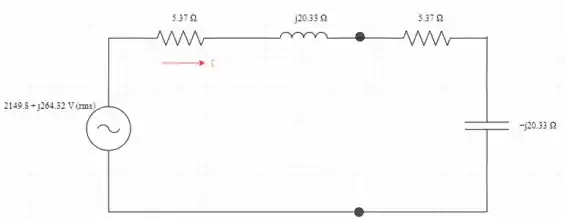
    Agora iremos determinar a tensão de Thevenin através dos terminais de carga

    V T h = j 64 I 1 + j 40 I 1

    = j 140 I 1

    = j 140 2.54 - j 20.67

    = 2149.8 + j 264.32     V r m s

    Iremos agora conectar os terminais de carga via curto-circuito como mostrado na figura. Teremos agora duas malhas para equacionarmos

    5120 = 30 I 1 + j 100 I 1 + j 40 I 1 - I s c + j 64 I 1 - I s c + j 40 I 1       ( 2 )

    0 = j 64 I s c - I 1 - j 40 I 1       ( 3 )

    De (3)

    I 1 = 8 13 I s c   ( 4 )

    Substituindo (4) em (2) para termos a corrente de curto-circuito I s c ,

    I s c = 38.25 - j 95.63   A ( r m s )

    Agora iremos determinar a impedância equivalente de Thevenin

    Z T h = V T h I s c

    =   2149.8   +   j 264.32 38.25   -   j 95.63

    = 5.37 + j 20.33 Ω

    A impedância de carga Z 0 na qual a potência média máxima é transferida para a carga é dada por

    Z 0 = Z T h *

    = 5.37 - j 20.33 Ω

    Agora conectando o equivalente de Thevenin a Z 0 como na figura. Iremos determinar a corrente que flui através da carga

    I   =   V T h R T h + R 0

    = 2149.8   +   j 264.32 10.74

    = 200.17 + j 24.61     A r m s

    Determinar agora a potência média máxima transferida para a impedância de carga

    P = I 2 R 0

    = 201.67 2 5.37

    = 218.4   k W

    Passo 2

  2. Aplicando Lei de Kirchoff no loop 2

    3. Z 0 I 2 + j 64 I 2 - I 1 - j 40 I 1 = 0

    Então,

    I 1 = Z 0 + j 64 j 104 I 2         ( 5 )

    Onde I 2 é a corrente que atravessa a carga, dado por

    I 2 = I

    = 200.17   +   j 24.61   A ( r m s )

    Substituindo por I 2 em (5) para podermos encontrar I 1

    I 1 = 5.37   -   j 20.33   + j 64 j 104 200.17 + j 24.61

    =   85.32 ∠ 0 º   A ( r m s )

    Infelizmente ainda não terminamos, agora iremos determinar a potência complexa desenvolvida pela fonte de tensão

    S d e v = 5120 ∠ 0 º I 1 *

    = 5120 85.32

    = 436.8   k V A

    Como a parte imaginária da potência complexa é zero, a potência média desenvolvida fornecida pela fonte P d e v é dada por

    P d e v = S d e v

    = 436.8   k W

    Passo 3

  3. A reatância de carga ótima X o p é dada por,

X o p = - X T h

= - j 20.33 Ω

Então a capacitância de carga ótima C o p é dada por

C o p = 1 ω X c

=   1 2 π 60 20.33

= 130.48   μ F

Do apêndice H, a capacitância mais próxima do valor é a de 100 μ F

C 0 = 100 μ F

Então a indutância de carga X0 é dada por

X 0 = - 1 2 π 60 100 ∙ 10 - 6

=   - 26.5258     Ω

A resistência de carga ótima R o p é dada por

R o p = ( R T h 2 + X 0 + X T h 2

=   5.37 2 + 20.33 - 26.5258 2

= 8.2 Ω

Do apêndice H, a resistência mais próxima é a de 10 Ω

R 0 = 10 Ω

Conecte a impedância de carga Z 0 ao circuito equivalente de Thevenin conforme mostrado na figura

I   = V T h Z T h + Z 0

=   2149.8   +   j 264.32 5.37   +   j 20.33   + 10   - j 26.5258

= 130.7 ∠ 28.96 º   A ( r m s )

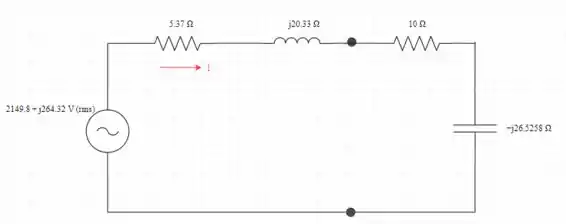
Agora é hora de determinar a potência

P = I 2 R 0

= 130.7 2 10

= 170.82   k W

A potência média transferida para a carga é de 170,82 kW em vez de 218,4 kW em (a)

C 0 = 100 μ F

R 0 = 10 Ω

Resposta

  1. P   =   218.4   k W
  2. P d e v = 436.8 k W
  3. C 0 = 100 μ F , R 0 = 10 Ω

Exercícios de Livros Relacionados

Calcule as impedâncias para as cargas no Ex. 12.5.1, se V e f i c a z = 240V
12.6. Calcule a potência media absorvida pelo resistor de 6-Ω.
Calcule a potência ativa, a potência reativa e a potência complexa entregue pela fonte.
Calcule a leitura do wattímetro
Calcule a potência média entregue ao resistor R