Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 96
A fonte de tensão no circuito da Figura P7.96(a) gera a forma de onda triangular mostrada na Figura P7.96(b). Suponha que a energia armazenada no capacitor seja nula em t = 0 e o amp op seja ideal.
a) Deduza as expressões numéricas para , para os seguintes intervalos de tempo: ; e .
b) Esboce a forma de onda de saída entre 0 e 4 .
c) Se a tensão de entrada triangular continuar a se repetir para , qual valor de tensão de saída poderemos esperar? Explique.
Passo 1
Faaala, galerinha!! Como vocês estão? Partiu resolver mais uma questãozinha?
Para essa questão aqui, vamos resolver primeiramente o item (a). Para isso, começaremos determinando a razão .
Como R e C foram dados no enunciado, temos que:
Passo 2
Para deduzirmos a expressão numérica para , no intervalo de , sabemos que .
Além disso, temos que
Resolvendo a expressão acima, temos:
Em
Passo 3
Já para deduzirmos a expressão numérica para , no intervalo de , sabemos que .
Além disso, temos que
Resolvendo a expressão acima, temos:
Em
Passo 4
Para finalizar o item (a), para deduzirmos a expressão numérica para , no intervalo de , sabemos que .
Além disso, temos que
Resolvendo a expressão acima, temos:
Em
Passo 5
Para esboçarmos a forma de onda de saída no intervalo pedido no item (b), basta usarmos os valores definidos para as expressões numéricas de . Desse modo, os valores utilizados para plotarmos o gráfico são:
Sendo assim, temos que:
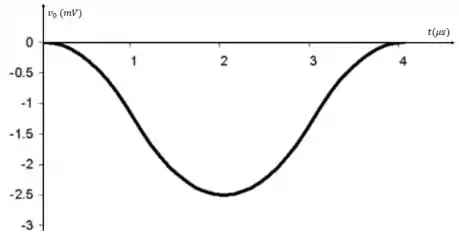
Passo 6
No item (c), podemos afirmar que a tensão de saída também se repetirá.
Isso decorre da observação de que em a tensão de saída é zero, portanto, não há energia armazenada no capacitor. Isso significa que o circuito está no mesmo estado em como estava em . Assim como se repete, também.
Prontinho, pessoal!! Bora resolver mais uma questão juntos?
Resposta
a) Em : ; em : ; em .
b)
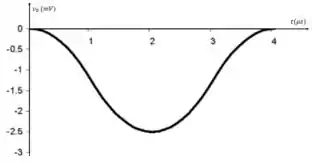
c) Resolução nos passos acima.