Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 47
Demonstre que um circuito em série é um filtro passa-baixa se a saída for extraída no resistor. Calcule a frequência de corte se e .
Passo 1
Galera, o circuito está representado abaixo:
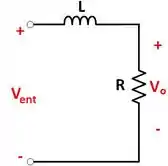
Pelo divisor de tensão,
Logo,
Passo 2
Se fizermos a frequência igual a , temos:
Agora, com , temos:
Como e , temos a prova de que o circuito é um filtro passa-baixa.
Passo 3
Por fim, para encontrarmos a frequência de corte, devemos usar a seguinte equação:
Substituindo os valores dados no enunciado:
Resposta
A frequência de corte é:
Exercícios de Livros Relacionados
Não há nenhuma energia armazenada no circuito da Figura P13.34 no instante em que a fonte de tensão é energizada. a) Determine Vo, Io e IL. b) Determine vo, i o e i L, para t $ 0
A chave do tipo liga-antes-interrompe-depois no circuito da Figura P13.39 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Determine i o , para t ≥ 0.
Não há nenhuma energia armazenada no circuito da Figura P13.25, no instante em que a chave é fechada. a) Determine v o , para t ≥ 0. b) Sua solução faz sentido em termos do comportamento conhecido do
Não há nenhuma energia armazenada no circuito na Figura P13.31 no instante em que a fonte de corrente é aplicada. a) Determine Ia e Ib. b) Determine ia e ib. c) Determine Va, Vb e Vc. d) Determine va,
Não há nenhuma energia armazenada no circuito da Figura P13.27, no instante em que a fonte de corrente é ligada. Dado que i g = 100u(t) A: a) Determine Io(s). b) Use os teoremas dos valores inicial e