Uma fonte trifásica equilibrada está fornecendo 540 kVA, com um fp atrasado de 0,96, a
duas cargas paralelas equilibradas ligadas em D. A impedância da linha de distribuição que
liga a fonte à carga é desprezível. A potência associada à carga 1 é 38,4 - j208,8 kVA.
a) Determine os tipos de componente e suas impedâncias por fase da carga 2, se a tensão
de linha for 1.600 V e os componentes da impedância estiverem em série.
b) Repita (a) com os componentes da impedância em paralelo.
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe circuitos trifásicos equilibrados!
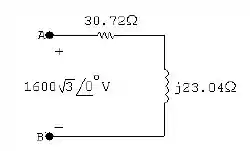
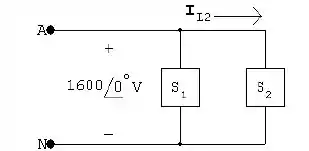
- Podemos ilustrar o sistema da seguinte forma:
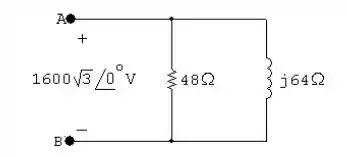
- Fazendo agora em paralelo temos que:
Para esse item, temos que:
Também:
No caso das correntes:
As indutâncias serão:
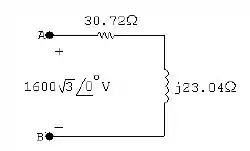
Passo 2
Sabendo que:
Agora seguem os cálculos finais:
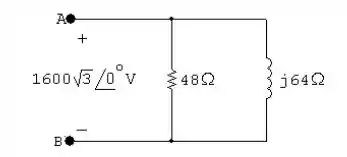
Resposta
- Item a:
- Item b: