Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 18
Para o sistema do Prob. 13.17, e a potência entregue à carga é . Calcule a corrente de linha e as tensões de fase da fonte, se for tomada como referência.
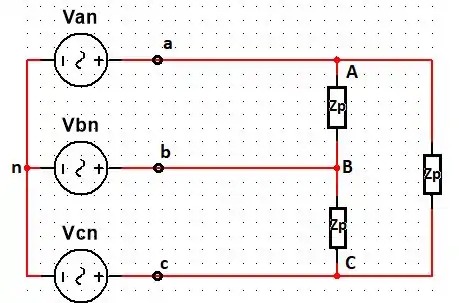
Passo 1
Mazoqueeee!! Mais uma de circuitinhos trifásicos?? So come here with me (aqui saaabe english... eu acho haha)! ;)
Primeiro a gente sabe que a potência em cada fase é:
Assim, temos que:
Em que:
- é a parte real de ;
- é a tensão de fase no lado das impedâncias em delta;
- é a potência em cada fase.
Assim, substituindo valores, temos:
Lembrando que:
Em que:
- é a tensão de linha no delta;
- é a tensão de linha no Y;
- é a tensão de fase nas fontes (lado Y).
Passo 2
Assim, tomando como referência (considerando seu fasor no ângulo ), temos:
Passo 3
Sabemos que a corrente de linha é dada por:
E que:
Assim, a corrente de linha é dada por:
Viu como não é um bicho de 7 cabeças? Bora pra mais outra!! ;)
Resposta
Exercícios de Livros Relacionados
No sistema Y - Δ equilibrado, a carga consome 3k W , com fator de potência 0.8 atrasado. Capacitores são conectados a cada fase da carga, para aumentar seu fator de potência para 0.9 atrasado. Calcule
11-O módulo da tensão de linha nos terminais de uma carga equilibrada, ligada em Y, é 6.600 V. A impedância de carga é 240 - j70 V/f. A carga é alimentada por uma linha cuja impedância é 0,5 + j4 V/f.
9-As expressões, no domínio do tempo, para as três tensões fase-neutro nos terminais de uma carga ligada em Y são vAN = 288 cos (vt - 45°) V,vBN = 288 cos (vt - 165°) V,vCN = 288 cos (vt + 75°) V.Quai
6-a) O circuito na Figura P11.6 é ou não um sistema trifásico equilibrado? Explique. b) Determine Io. Figura P11.6
As três ferramentas descritas a seguir fazem parte da oficina de uma universidade. Cadaferramenta é uma carga trifásica equilibrada com tensão nominal de 220 V (ef). Calcule (a)o módulo da corrente de