Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 20
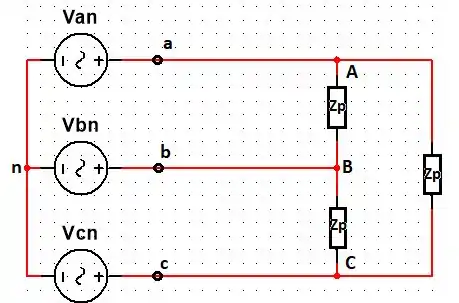
No sistema do Prob. 13.17, a tensão da fonte, (eficazes) e . Calcule a tensão de linha, a corrente de linha, os módulos da corrente da carga e a potência entregue à carga.
Passo 1
Veeeem aqui que essa questão é super mega hiper master simples!!! Se ligaa:
A gente sabe que a tensão de linha (no Y) é dada por:
Como a tensão de fase é . Looogo, a tensão de linha (eficaz) é:
Passo 2
A corrente de linha (no )é:
E a corrente de fase no delta é:
Portanto, é:
Passo 3
A potência entregue a carga é dada por:
Simples, ligeirinha e direta né?? Bora pra próxima!!
Resposta
Exercícios de Livros Relacionados
Se, na Fig, 13.4, V a = V ab 1000 p V (eficazes), a impedância entre os terminais A - N e 10 , 60 ∘ , Ω , e a entre os terminais N - B e 10 - 60 r Ω , calcule a corrente de neutro I s v ∘
Na Fig. 13.5, façamos V 1 = 1000 e V (eficazes). Z 1 = 5 + 15 Ω 1 Z 2 = 0,5 Ω , Z 3 = 1 Ω e Z 4 = 10 - j 5 Ω . Calcule a poténcia média absorvida pelas cargas, dissipada nas linhas e entregue pelas fo
No sistema Y + Δ mostrado na figura, a fonte é de seqüência positiva c o m V a n = 1000 ∘ V (eficazes) e a impedância de fase é Z p = 3 - j4 Ω . Calcule a tensão de linha V L , a corrente de linha I
Uma fonte trifásica equilibrada, de sequência positiva, c o m V o = 20000 ∘ V (eficazes), está alimentando uma carga conectada e m Δ , Z A B = 20 Ω , Z B C = 20 / 60 ∘ Ω e Z C A = 50 / 30 ∘ Ω . Calc
Uma fonte trifásica equilibrada, de sequência positiva, com V a b - 20000 ° (eficazes) está alimentando uma carga conectada e m Δ , Z A B = 50 Ω , Z B C = 20 + j 20 Ω eZ C A = 30 - j 40 Ω . Calcule as