Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 30
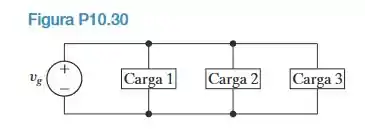
As três cargas do circuito da Figura P10.30 podem ser descritas da seguinte forma: a carga 1 é um resistor de em série com uma reatância indutiva de ; a carga 2 é uma reatância capacitiva de em série com um resistor de ; e a carga 3 é um resistor de em série com uma reatância capacitiva de . A frequência da fonte de tensão é 60 Hz.
a) Determine o fator de potência e o fator reativo de cada carga.
b) Determine o fator de potência e o fator reativo da carga composta vista pela fonte de tensão.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - A impedância da primeira carga é dada por
Passando para fasores
A diferença de fase entre a primeira tensão de carga e a corrente é dada por
Determinando o fator de potência da primeira carga
Como a primeira corrente de carga está atrasada em relação à tensão, o primeiro fator de potência de carga está atrasado
Determinando a potência reativa da primeira carga
Passo 2
Agora, a impedância é dada por
Em fasores, nós temos que
A diferença de fase entre a segunda tensão de carga e a corrente é dada por
Determinando o fator de potência, nós temos que
Como a segunda corrente de carga lidera a tensão, o segundo fator de potência de carga está liderando
Determinando a potência reativa na segunda carga
Com isso, nós temos que
A impedância da terceira carga é dada por
Convertendo para fasores,
A diferença de fase entre a terceira tensão de carga e a corrente é dada por,
Passo 3
Determinando o fator de potência na terceira carga
Com isso, nós temos que
Como a terceira corrente de carga lidera a tensão, o terceiro fator de potência de carga está liderando
A potência reativa é dada por
Com isso,
Passo 4
B - As três cargas são conectadas em paralelo para determinar a impedância equivalente das cargas, é mais fácil determinar primeiro a admitância de cada carga, determinando a admitância da carga 1.
Com isso, nós obtemos o seguinte resultado
Para o caso da admitância da carga 2
Com isso, nós temos que
Determinando a admitância da carga 3
Substituindo os valores,
Agora, nós já podemos determinar a admitância equivalente
Substituindo os resultados
Portanto,
Agora, fazendo o inverso e determinando a impedância equivalente
Com isso,
Para as fasores,
Passo 5
A diferença de fase entre a tensão e a corrente de carga composta é dada por
Determinando o fator de potência da carga composta
Com isso, nós temos que
Como a corrente de carga composta lidera a tensão, o fator de potência de carga composta está adiantado.
Determinando a potência reativa da carga composta
Com isso,