Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 37
37-
Resolva o Problema 4.25 usando o método das correntes de malha.
Passo 1
Então, vamos enfrentar essa fera... brincadeira rsrs. Essa questão é bem tranquila, basta que a gente pense um pouquinho. Vamos analisar o circuito abaixo e arrasar?!
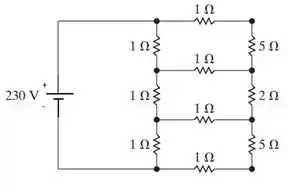
Figura P4.25
a)
Utilizando o método das correntes de malha, a gente constrói as seguintes equações:
−230 + 1(i1 − i2) + 1(i1 − i3) + 1(i1 − i4) = 0
6i2 + 1(i2 − i3) + 1(i2 − i1) = 0
2i3 + 1(i3 − i4) + 1(i3 − i1) + 1(i3 − i2) = 0
6i4 + 1(i4 − i1) + 1(i4 − i3) = 0
Passo 2
Passando as equações para a forma padrão:
i1(3) + i2(−1) + i3(−1) + i4(−1) = 230
i1(−1) + i2(8) + i3(−1) + i4(0) = 0
i1(−1) + i2(−1) + i3(5) + i4(−1) = 0
i1(−1) + i2(0) + i3(−1) + i4(8) = 0
Após a gente resolver as equações, temos os seguintes resultados:
i1 = 95 A;
i2 = 15 A;
i3 = 25 A;
i4 = 15 A
A potência consumida pelo resistor de 5Ω:
p5 = i32*(2) = (25)2*(2) = 1250W
Passo 3
b) Agora é só calcular a potência da fonte e correr pro abraço!!!
p230 = −(230)i1 = −(230)*(95) = −21850W
Resposta
a) 1250W.
b) −21850W.