Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 10
Mostre que, no caso geral, o circuito do Prob. 15.4 é um filtro passa-faixa com frequência central rad/s, largura da faixa rad/s, ganho e índice de mérito . Faça , e para obter a função de rede
Passo 1
Eaeee. Seguinte, do Prob. 15.4 temos o seguinte circuito:
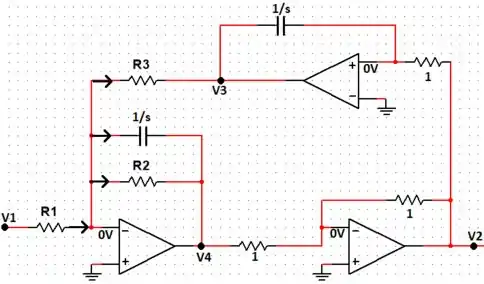
Passo 2
Também, do Prob. 15.4, descobrimos que a função de rede é dada por:
Passo 3
Fazendo para, temos (levando em conta que ):
Assim, para , temos que:
Passo 4
Nesse sentido, lembrando que:
Logo, temos que:
E o ganho é dado por:
Resposta
Exercícios de Livros Relacionados
Usando fasores, determine: 3 cos ( 20 t + 10 ° ) - 5 cos ( 20 t - 30 ° ) 40 s e n 50 t + 30 c o s( 50 t - 45 ° ) 20 s e n 400 t + 10 cos ( 400 t + 60 ° ) - 5 s e n ( 400 t - 20 ° )
Usando fasores, determine: 3 cos ( 20 t + 10 ° ) - 5 cos ( 20 t - 30 ° ) 40 s e n 50 t + 30 c o s( 50 t - 45 ° ) 20 s e n 400 t + 10 cos ( 400 t + 60 ° ) - 5 s e n ( 400 t - 20 ° )
Usando fasores, determine i ( t ) nas seguintes equações: 2 d i d t + 3 i t = 4 cos ( 2 t - 45 ° ) 10 ∫ id t + d i d t + 6 i t = 5 cos ( 5 t + 22 ° )
Aplique análise fasorial para calcular o seguinte: v = 110 sen 20 t + 30 ° + 220 cos 20 t - 90 °V i = 30 cos 5 t + 60 ° - 20s e n 5 t + 60 °A
Obtenha as senoides correspondentes a cada um dos seguintes fasores: V 1 = 60 ∠ 15 °V ,ω = 1 V 2 = 6 + j 8V ,ω = 40 I 1 = 2,8 e - j π / 3A ,ω = 377 I 2 = - 0,5 - j 1,2A ,ω = 10 3