Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 20
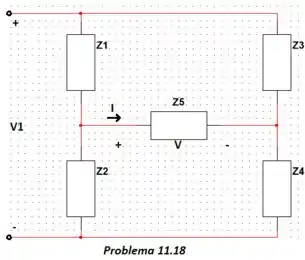
Note que o circuito fasorial correspondente é uma ponte equilibrada e use o método do Prob. 11.18, com substituído por um circuito aberto, para encontrar a resposta forçada .
Passo 1
Eaeee.. eita que a questão pede pelo método lá do Problema 18 que a gente fez anteriormente. Então só booraaa!!
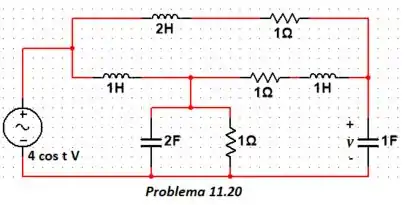
Seguinte... Vamos primeiro passar os valores da fonte para a forma polar e enxergar os capacitores e os indutores em forma de reatâncias.
Lembrando que:
Em que .
Logo, temos:
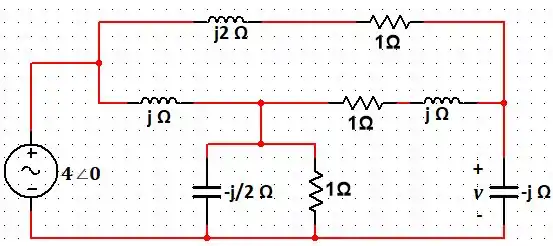
Passo 2
Agora, vamos fazer como a questão pede. Bora deixar o circuito com as impedâncias organizadas como no Problema 18. Também já vamos deixar a impedância como um circuito aberto. Assim temos:
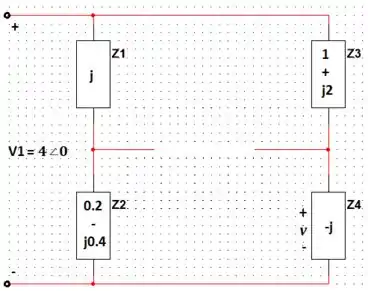
Passo 3
Bora agora fazer como a gente já fez em um bocado de problemas passados hehe. Vamos selecionar os seguintes nós e atribuir direções da corrente e também vamos colocar o terra (referencial de potencial 0 V) na parte de baixo do circuito para facilitar nossa vida:
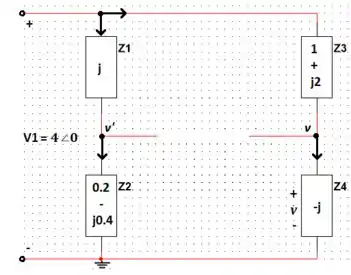
Passo 4
Pelo método da questão 18, temos que Quer ver???
Se ligaa:
Utilizando a Lei dos Kirchhoff das Correntes para descobrir , temos:
Agora, utilizando a Lei dos Kirchhoff das Correntes para descobrir , temos:
Viu como a ponte equilibrada pode facilitar muito nossa vida?? Massa demais ;)