Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 14
Calcule a tensão em regime permanente.
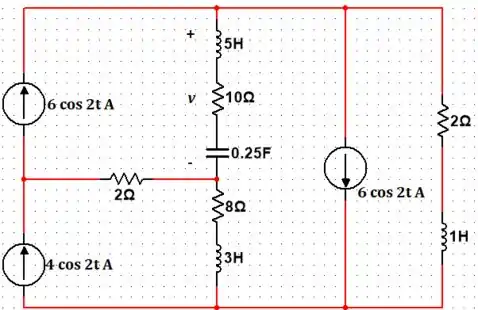
Passo 1
Psiu!! Olha o spoiler: superposiçãoo!!
Mas aaaantes, bora primeiro passar os valores das fontes para a forma polar e enxergar o capacitores e os indutores em forma de reatâncias.
Lembrando que:
Em que .
Logo, temos:
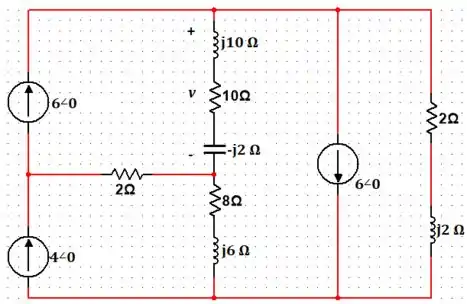
Passo 2
Podemos descobrir o valor de aplicando o teorema da superposição. Vc faz primeiro a corrente do circuito somente abastecido pela fonte de da esquerda e depois faz a mesma coisa somente com as outras fontes separadamente. Aí, por fim, a gente soma os três valores de tensão!!
Obs: quando for excluir as outras fontes de corrente durante a análise, trate-as como circuitos abertos.
Ficou confuso né?? Então vem aqui ;)
Primeiro vamos fazer com a fonte de da esquerda:
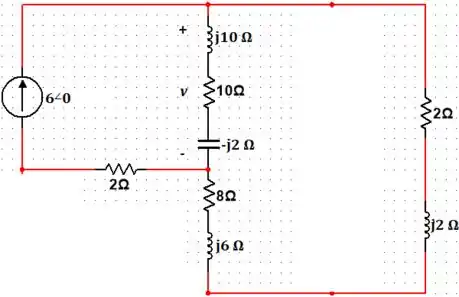
Somando as impedâncias em série, temos:
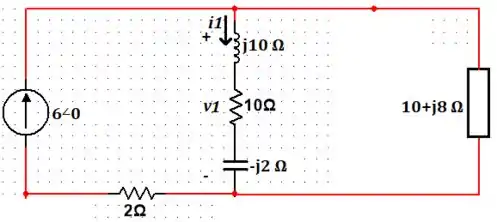
Aplicando o divisor de corrente, temos que:
Assim, pela Lei de Ohm, temos que é:
Passo 3
Agora, para a fonte de :
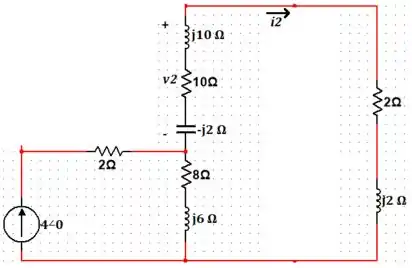
Aplicando o divisor de corrente já somando as impedâncias em série, temos que:
Assim, pela Lei de Ohm, temos que é:
Passo 4
Por fim, para a fonte de da direita:
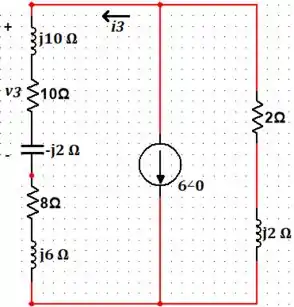
Aplicando o divisor de corrente já somando as impedâncias em série, temos que:
Assim, pela Lei de Ohm, temos que é:
Passo 5
Agora é só somar os valores das tensões que descobrimos haha. Se liga: