Para o circuito da figura, calcule para .
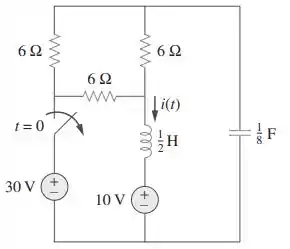
Passo 1
Para o indutor funciona como um curto circuito e o capacitor funciona como um circuito aberto, então temos:
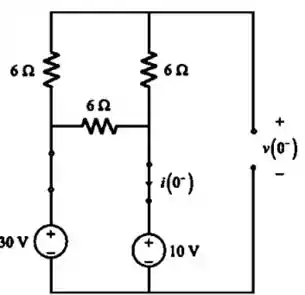
Passo 2
Agora, vamos calcular a resistência equivalente:
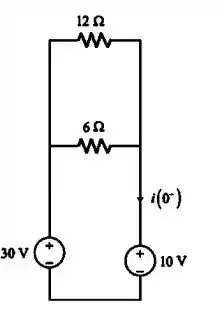
E em seguida, fazendo o paralelo:
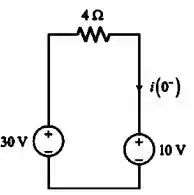
Passo 3
Vamos calcular a corrente e como no indutor não pode haver mudanças repentinas na corrente, temos:
Passo 4
Vamos encontrar a tensão utilizando a lei das correntes de Kirchhoff no nó :
A tensão , pois no capacitor, não pode haver mudanças repentinas de tensão.
Passo 5
Agora, vamos passar esse circuito simplificado para o domínio de Laplace incluindo as condições iniciais:
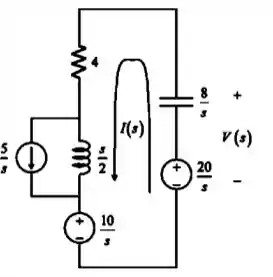
Passo 6
Aplicando a Lei das Correntes de Kirchhoff nesta figura, conseguimos isolar o
Passo 7
Separando em frações parciais teremos:
Agora basta encontrar
Daí, substituindo, teremos:
Por Laplace utilizando a tabela de transformadas, teremos: