Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 51a
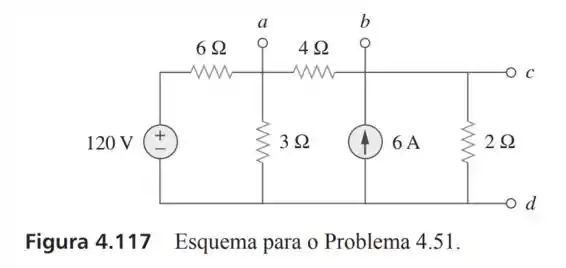
51- Dado o circuito da Figura , obtenha o equivalente de Norton conforme visto dos terminais:
Passo 1
Para a letra , primeiro devemos tirar as fontes independentes para calcular a resistência de Norton entre os pontos . A fonte de tensão substituiremos por um curto-circuito enquanto a fonte de corrente substituiremos por um circuito aberto.
Se retirarmos as fontes independentes, nós ficaremos com a seguinte malha resistiva em volta dos contatos :
Dessa forma vemos que as resistências de e de estão em paralelo nos dando uma resistência equivalente de:
E que por sua vez essa resistência equivalente está em série com a resistência de
Então temos no final um resistor de em paralelo com outro resistor de :
Dessa forma o será de:
Passo 2
Agora vamos encontrar a corrente de Norton que passa na linha quando fechamos circuito entre esses dois pontos.
Note, que quando fechamos circuito em nenhuma corrente passará pelo resistor de , pois a corrente prefere o caminho com menor resistência, nesse caso o caminho com menor resistência é entre os pontos a e b. Nos deixando com o seguinte circuito:
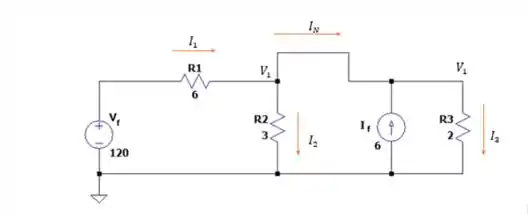
Fazendo a somatória das correntes que entram no nó teremos:
Lembrando que as correntes podem ser escritas como:
Ou seja, sempre devemos subtrair a tensão de onde a corrente sai da tensão pra onde a corrente entra. Por exemplo, a corrente será:
Substituindo os valores:
Vamos fazer o mesmo para :
Nesse caso como o ponto onde a corrente entra é o nó de terra, a tensão desse ponto é igual a zero. Logo:
Vamos reescrever as correntes , e :
Passo 3
E sabendo que a tensão no resistor de vale , teremos também a somatória de correntes no nó da fonte de corrente:
Para determinar a corrente , nós devemos fazer o mesmo que fizemos com :
Logo substituindo na expressão anterior:
Passo 4
Logo podemos igualar as duas equações de :
Então a corrente de Norton será de:
É sempre meio doido quando uma corrente flui em uma linha que não há diferença de tensão, mas é exatamente isso que acontece quando colocamos fontes de correntes ou mais de uma fonte.