Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 66
66- Obtenha a potência média absorvida pelo resistor de no circuito com Figura
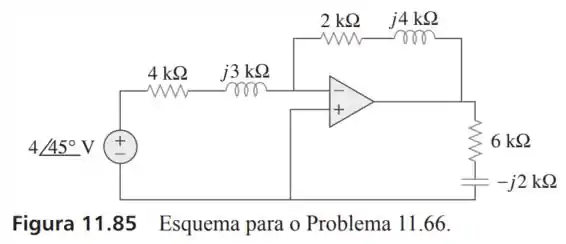
Passo 1
Os mesmos comportamentos vistos para tensão contínua também são vistos para corrente alternada. Então, sabendo que esse circuito é o esquema de um amplificador inversor temos que a tensão de saída dessa amplificador será:
Dessa forma:
Fazendo o fasor das duas impedâncias teremos:
Passo 2
Agora vamos encontrar a potência complexa que essa tensão gera na carga.
Dessa forma a potência real (ou média ) será:
Lembrando sempre que o ângulo de defasagem da tensão não interfere na potência.
Resposta
Exercícios de Livros Relacionados
Para um circuito equivalente de Thévenin constituindo de uma fonte de tensão V g e uma impedância Z g = R g + j X g ;A – Mostre que o circuito entrega a potência máxima para a carga Z L = R L + J X L
Repita o Ex. 12.4.2, usando o conceito de potência complexa.
Suponha que o coeficiente de acoplamento no circuito da Figura P10.56 seja ajustável.a) Determine o valor de k que torne v o igual a zerob) Determine a potência desenvolvida pela fonte quando k tem o
A fonte de tensão senoidal no circuito da Figura P10.40 está fornecendo uma tensão eficaz de 2.000 VA carga de 4 V está absorvendo quatro vezes mais potência média do que a carga de 25 V. As duas carg
a) Admita que, na Figura P10.48, R o possa variar entre 0 e 10 kV. Repita (b) e (c) do Problema 10.48.b) A nova potência média calculada em (a) é maior do que a determinada no Problema 10.48(a)?c) A n