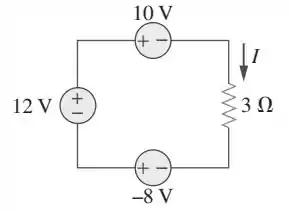
A partir do circuito da figura 2.83 , determine I , a potência dissipada pelo resistor e a potência fornecida por cada fonte.

I = - 2 A P r = 12 W P - 8 V = 16 W P 12 V = - 24 W P 10 V = 20 W

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 19

A partir do circuito da figura , determine , a potência dissipada pelo resistor e a potência fornecida por cada fonte.

Passo 1

Dá uma olhadinha no circuito:

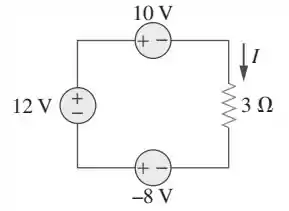
Para resolver essa questão, vamos usar a lei de Kirchoff para tensões. O que a gente vai fazer é o seguinte: vamos caminhar pelo circuito somando e subtraindo tensões e voltar para o mesmo ponto. Qual é a diferença de tensão entre um ponto e ele mesmo? Só pode ser zero! Lembra do seguinte: se passar do menos pro mais na fonte de tensão, soma a tensão, e se passar do mais pro menos, subtrai. Além disso, se a gente passar a favor da corrente no resistor, a tensão abaixa, e se passar contra a corrente, ela aumenta.

Passo 2

Vamos começar dando a volta no circuito, no sentido horário, junto com essa corrente , e voltar para o mesmo ponto. Bora lá!

Passo 3

Agora vamos para as potências dissipadas: na fonte, a potência é dada por , enquanto no resistor ela vale . Vamos então. No resistor:

E nas fontes:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tabela da Figura P2.30(a) mostra a relação entre a tensão e a corrente nos terminais da fonte real de corrente constante representada na Figura P2.30(b).a) Faça um gráfico de i s versus v s .b) Cons

Deduza a Equação 2.25. Sugestão: use as equações (3) e (4) do Exemplo 2.11 para expressar i E como uma função de i B. Resolva a Equação (2) para i 2 e substitua o resultado nas equações (5) e (6). Res

As correntes i a e i b no circuito da Figura P2.26 são 4 A e -2 A, respectivamente. a) Determine i g. b) Determine a potência dissipada em cada resistor. c) Determine vg. d) Mostre que a potência forn

Para o circuito mostrado na Figura P2.36, calcule i ∆ e v σ e (b) mostre que a potência fornecida é igual à potência absorvida.

Para o circuito mostrado na Figura 2.24, R1 = 40 kV, R2 = 60 kV, RC = 750 V, RE = 120 V, VCC = 10 V, V0 = 600 mV e β = 49. Calcule iB, iC, iE, v3d, vbd, i2, i1, vab, iCC e v13. (Observação: na notação