Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 17
a) Projete um circuito RLC em paralelo (veja a Figura 8.1) usando valores de componentes do Apêndice H, com uma frequência angular de ressonância de 5.000 rad/s. Escolha um resistor ou crie uma rede de resistores de modo que a resposta seja criticamente amortecida. Desenhe seu circuito.
b) Calcule as raízes da equação característica para a resistência em (a).
Passo 1
Faaaaala, pessoal!! Bora resolver mais uma questão juntos?
Para essa questãozinha aqui, observamos que o enunciado deu o valor da frequência angular de ressonância (). Sendo assim, podemos iniciar o item (a) determinando a seguinte relação:
Além disso, vemos que a partir do foi pedido no enunciado do item (a), temos várias possíveis soluções. Começaremos escolhendo . Então:
Podemos alcançar esse valor de capacitor usando componentes do apêndice H combinando quatro capacitores de em paralelo.
Passo 2
Para que o enunciado seja satisfeito, devemos ter um circuito cuja resposta seja criticamente amortecida, ou seja, que .
Nós sabemos também que . Como C foi encontrado no passo anterior, teremos:
Passo 3
Para finalizarmos o item (a), podemos criar esse valor de resistor encontrado acima usando os componentes do apêndice H, combinando um resistor de e um resistor de em série.
Desse modo, teremos como circuito final:
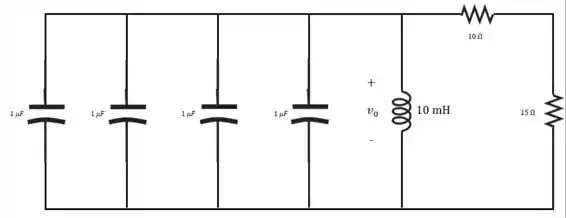
Passo 4
Já para calcular as raízes, a partir do valor da resistência do item (a), utilizaremos a seguinte fórmula:
Sendo assim, como :
Portanto, existem duas raízes reais repetidas em .
Prontinho, pessoal!! Bora resolver mais uma questão juntos?
Resposta
a)
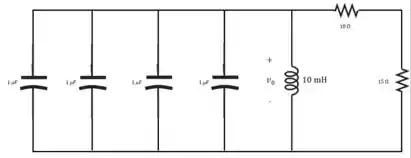
b) Existem duas raízes reais repetidas em .