Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 39

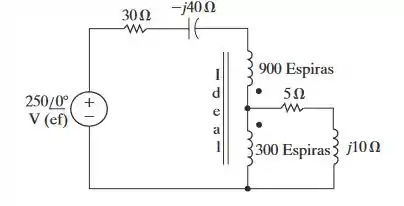
a) Determine a potência média dissipada em cada resistor no circuito da Figura P10.39.

b) Confirme sua resposta demonstrando que a potência total fornecida é igual à potência total absorvida.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Como mostrado no circuito do enunciado, ele tem duas malhas, então aplicando a LKT na malha 1, nós temos que

250 = 30 - j 40 I 1 + V 1 + V 2   1

E na malha 2, nós obtemos o seguinte resultado

0 = 5 + j 10 I 2 - V 2   ( 2 )

A relação das tensões das bobinas de 900 e 300 espiras é dada por

V 1 900 = - V 2 300

Portanto,

V 1 = - 3 V 2   ( 3 )

Já a relação de correntes é dada por

900 I 1 = 300 I 1 - I 2

Logo, nós temos que

I 2 = - 2 I 1   ( 4 )

Passo 2

Substituindo o (3) em (1), e o (4) em (2) respectivamente

250 = 30 - j 40 I 1 - 2 V 2     5

E

0 = - 10 - j 20 I 1 - V 2   ( 6 )

Resolvendo (5) e (6) de forma simultânea, nós temos que

I 1 = 5   A r m s

E

V 2 = - 50 - 100 j   V ( r m s )

E de (3) e (4)

V 1 = 150 + j 300   V r m s

E também

I 2 = - 10   A ( r m s )

Passo 3

Determinando a potência média dissipada no resistor de 30   Ω , nós temos

P 30 Ω = I e f 2 R

Fazendo a substituição, nós temos que

P 30 Ω = 5 2 30 = 750   W

E no resistor de 5   Ω

P 5 Ω = I e f 2 R

Novamente, substituindo os valores

P 5 Ω = 10 2 5 = 500

Portanto,

P 30 Ω = 750   W   e   P 5 Ω = 500   W

Passo 4

B – Primeiro, vamos determinar a potência média total dos resistores

∑ P a b s = P 30 Ω + P 5 Ω

Fazendo a substituição

∑ P a b s = 750 + 500 = 1250   W

E agora, vamos saber sobre a potência complexa gerada pela fonte de tensão

S g = - V e f I e f *

Com isso,

S g = - 250 5 = - 1250   V A   7

Como a parte imaginária de potência complexa da fonte é zero, então

P g = S g = - 1250   W

Portanto, a potência total desenvolvida é igual à potência total absorvida

Resposta

a )   P 30 Ω = 750   W   e   P 5 Ω = 500   W

b )   A   p o t ê n c i a   t o t a l   d e s e n v o l v i d a   é   i g u a l   à   p o t ê n c i a   t o t a l   a b s o r v i d a

Exercícios de Livros Relacionados

O valor de pico da tensão da fonte senoidal do circuito da Figura P10.48 é 180 V, e sua frequência é 5.000 rad/s. O resistor de carga pode variar de 0 a 4.000 V e o capacitor de carga pode variar de 0
a) Determine a relação de espiras N1/N2 do transformador ideal, no circuito da Figura P10.63, de modo que uma potência média máxima seja fornecida à carga de 400 V. b) Determine a potência média forne
A impedância ZL no circuito da Figura P10.54 é ajustada para máxima transferência de potência média a ZL. A impedância interna da fonte de tensão senoidal é 4 + j7 V. a) Qual é a máxima potência média
O resistor de 160 V no circuito da Figura P10.51 é substituído por uma impedância variável Zo. Admita que Zo seja ajustada para transferência de máxima potência média. a) Qual é a máxima potência médi
Determine a expressão de regime permanente para as correntes i g e i L no circuito da Figura P10.55, quando vg = 400 cos 400t V.Determine o coeficiente de acoplamento. c) Determine a energia armazenad