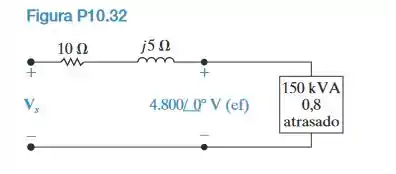
A queda de tensão de regime permanente ao longo da linha de transmissão da Figura P10.32 é excessiva. Um capacitor é colocado em paralelo com a carga de 150 kVA e ajustado até que a tensão de regime permanente no início da linha tenha a mesma magnitude que a tensão na carga, isto é, 4.800 V (ef). A carga de 150 kVA está operando com um fator de potência atrasado de 0,8. Calcule o valor do capacitor, em microfarads, se o circuito estiver operando em 60 Hz. Quando selecionar o capacitor, não se esqueça da necessidade de manter a perda de energia da linha em um nível razoável.

Determinando a corrente fluindo através da carga

Com isso, nós temos que

Transformando em fasores, nós obtemos o seguinte resultado

Já a corrente no capacitor é dado por

E com isso,

Portanto, a corrente fornecida para a carga e o capacitor é dado por

Desenvolvendo um pouco mais

A tensão é dado por

Substituindo , nós obtemos que

Desenvolvendo os termos

Utilizando a propriedade associativa

A magnitude da tensão de é igual a

Portanto,

Substituindo os valores, nós temos que

Portanto,

Resolvendo (1) para determinar o valor de K

E

Para manter a perda na linha o menor possível, vamos selecionar o menor valor de K.

Determinando o valor da reatância do capacitor

Fazendo a substituição

Portanto,

E com isso, o valor do capacitor é igual a

Logo, temos que