Calcule a tensão em regime permanente v , usando o circuito fasorial.

v t = 4 cos ⁡ 8 t - 53,13 °V

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.9 - Ex. 2

Calcule a tensão em regime permanente , usando o circuito fasorial.

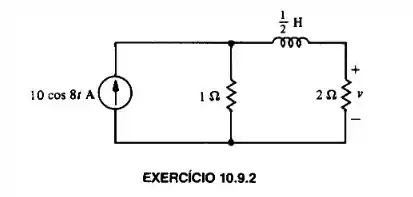
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Para essa questão, nós não mexer no resistor de , visto que modificaria a tensão, mas podemos utilizar uma transformação de fontes, logo o circuito dessa maneira

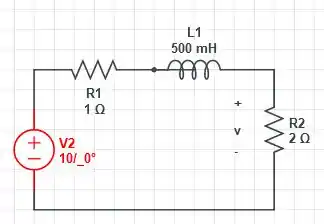
Podemos fazer o equivalente entre o resistor de e o indutor (que nesse caso convertido para fasor é igual a ), logo, temos um divisor de tensão para encontrar (isso mesmo, bem simples), mas vamos deixar isso para o próximo passo.

Passo 2

O divisor de tensão é dado da seguinte forma

Agora, vamos entender por

Portanto, temos que

Logo, temos que é igual a

Desenvolvendo um pouco mais...

Passando para o domínio do tempo, nós obtemos

Resposta

Exercícios de Livros Relacionados

Determine os fasores correspondentes aos seguintes sinais: v t = 21 cos ⁡ 4 t - 15 °V i t = - 8 s e n10 t + 70 °m A v t = 120 s e n10 t - 50 °V i t = - 60 cos ⁡ ( 30 t + 10 ° )m A

Calcule os números complexos a seguir e deixe seus resultados na forma polar: 5 ∠ 30 ° 6 - j 8 + 3 ∠ 60 ° 2 + j 10 ∠ 60 ° 35 ∠ - 50 ° 2 + j 6 - ( 5 + j )

Calcule os números complexos a seguir e expresse seus resultados na forma retangular: 60 ∠ 45 ° 7,6 - j 10 + j 2 32 ∠ - 20 ° ( 6 - j 8 ) ( 4 + j 2 ) + 20 - 10 + j 24 20 + ( 16 ∠ - 50 ° ) ( 5 + j 12 )

Determine os fasores correspondentes aos seguintes sinais: v t = 21 cos ⁡ 4 t - 15 °V i t = - 8 s e n10 t + 70 °m A v t = 120 s e n10 t - 50 °V i t = - 60 cos ⁡ ( 30 t + 10 ° )m A

Calcule os números complexos a seguir e deixe seus resultados na forma polar: 5 ∠ 30 ° 6 - j 8 + 3 ∠ 60 ° 2 + j 10 ∠ 60 ° 35 ∠ - 50 ° 2 + j 6 - ( 5 + j )