Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 5.Problemas - Ex. 28

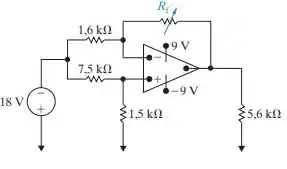
O resistor Rf no circuito da Figura P5.28 é ajustado até que o amp op ideal se sature. Especifique Rf em quilo-ohms.

Passo 1

Falaiii meus amores, cêis tão suave?

Bora pra mais uma??

Então, encostaa!!

Consultando a figura P5.28 do livro de texto para o diagrama de circuito. Aplicando a divisão de tensão para encontrar a tensão no terminal não inversor

Devido ao conceito de terra virtual, a tensão no terminal não inversor é igual à tensão no terminal inversor. Portanto,

Aplicando a lei das correntes de Kirchhoff no terminal inversor

Passo 2

Se a magnitude da tensão da fonte for maior que a razão entre a tensão da fonte de alimentação e o ganho de malha fechada, então o amplificado operacional ideal simplesmente satura. A condição para saturação do amplificador operacional ideal é

Sob a condição de saturação, a tensão de saída do circuito do amplificador operacional torne-se igual à tensão da fonte de alimentação.

Substituía o valor das tensões de alimentação para encontrar a faixa de , para trabalhar o op-amp na região linear .

Substitua

Passo 3

Substituindo

Resistências negativas não são usadas, então o valor máximo de pode ser ajustado para fazer com que o amplificador operacional na região linear seja .

Resposta

Resistências negativas não são usadas, então o valor máximo de pode ser ajustado para fazer com que o amplificador operacional na região linear seja .

Exercícios de Livros Relacionados

Empregue o método do Prob. 3.17 para construir uma resistência negativa de -6Ω, onde a potência dissipada em R 1 é 2W quando v 1 = 6 V .

Se Rf = R1 = 1 k Ω no circuito do Prob. 3.29, calcule os valores dos demais resistores de forma que Vo = V1 + V2. (Note que o resultado é verdadeiro se R = Rf = R1 = R2.)

Um amp. op. nõo-ideal mostrado em (a) pode ser representado pelo modelo de (b), onde A é um ganho muito elevado, da ordem de 10^5 . Para amp. op de alta qualidade, o ganho deve ser muito maior, da ord

Calcule Vo em termos das tensões de nó V1, V2, e V3) e das resistências. (Este circuito é um somador, como o do Prob. 3.14, com uma fonte de tensão adicional.)

Calcule i.