Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.5 - Ex. 4

Resolva o Ex. 8.5.3., se i_g = 13 cos (t) A

Passo 1

E aí meus amigos? Tudo bem com vocês? O Corazon vai ajudar vocês nesta questão. Boraaaaa!

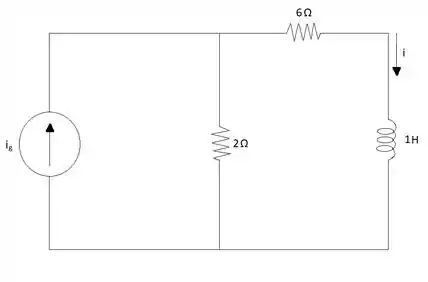
Esta questão do Johnson apresenta o mesmo circuito da questão anterior a ela e a única coisa que mudou é o valor da fonte de corrente. Dito isso, podemos dar continuidade à resolução da questão tendo o mesmo início que a questão anterior, fazendo a análise de malhas:

i_1 = i_g = 13 cos (t) A

2 (i_2 - i_1) + 6 i_2 + (d i_2)/(d t) = 0

Realizando a substituição do valor da corrente i_1 na equação obtemos a seguinte expressão:

(d i_2)/(d t) + 8 i_2 = 26 c o s ( t )

Passo 2

Visto que caímos numa equação diferencial com um valor mais complexo na igualdade devemos recorrer às resoluções que o cálculo no dá para este tipo de equação. Visto que caímos numa equação diferencial de primeira ordem se usa a técnica de fator integrante para resolvê-la. Como o objetivo é resolver apenas a parte de elétrica da questão iremos pular essa resolução e o resultado é o seguinte:

i_2 ( t ) = 0,4 [s e n (t) + 8 cos (t)] + C e^(- 8 t)

Passo 3

Para finalizar a resolução desta questão é preciso encontrar o valor da constante C que aparece na expressão anterior e para isso usamos o valor de i (0) = 4 A que foi dita no enunciado da questão:

4 = 3,2 + C

C = 0,8

Com o valor de C encontrado, agora só devemos substituir na expressão que foi encontrada antes:

i_2 ( t ) = 0,4 [s e n (t) + 8 cos (t)] + 0,8 e^(- 8 t)

i_2 ( t ) = 0 , 4 [8 cos (t) + s e n (t) + 2 e^(- 8 t)] A

Legal! A questão está resolvida.

Resposta

i ( t ) = 0,4 [8 cos (t) + s e n (t) + 2 e^(- 8 t)] A

Exercícios de Livros Relacionados

Determine i L (t) e a energia total dissipada pelo circuito a seguir de t = 0 a t = ∞ s. O valor de v i n (t) é igual a [40– 40u(t)] V.
Se o pulso de entrada na Figura 7.130a for aplicado ao circuito da Figura 7.130b, determine a resposta i(t).
Para o circuito da Figura 7.127, calcule i(t) se i(0) = 0.
Obtenha v(t) e i(t) no circuito da Figura 7.128.
A resistência de uma bobina de 160m H é igual a 8Ω . Determine o tempo necessário para a corrente chegar a 60 % de seu valor final quando a tensão é aplicada à bobina.