Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 13

O resistor no circuito da Figura P8.11 é reduzido de 50 Ω para 32 Ω . Determine v 0 ( t ) para t ≥ 0 .

Passo 1

Faaaaala, pessoal!! Bora resolver mais uma questão juntos?

Para essa questãozinha aqui, devemos primeiro fazer a análise do circuito em duas situações: em t < 0 e em t > 0 .

Na primeira situação ( t < 0 ), teremos o seguinte cenário:

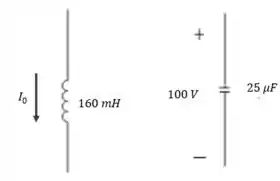
Portanto, temos que V 0 = 100   V , e que o valor de I 0 será o que está no circuito do enunciado: 5 A.

Na segunda situação ( t > 0 ) temos o seguinte:

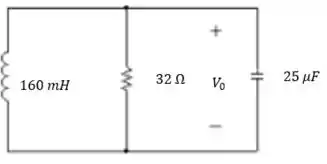
Passo 2

Agora que já temos os dois cenários possíveis para os valores de t, vamos analisar a resposta do circuito, para determinar a equação geral de v 0 ( t ) .

Para isso, basta fazermos a comparação entre os valores de α e   ω 0 : Se α 2 > ω 0 2 , o circuito é superamortecido. Se α 2 < ω 0 2 , o circuito é subamortecido. E se α 2 = ω 0 2 , o circuito é criticamente amortecido.

Sendo assim, calcularemos primeiro os valores de α e   ω 0 :

Para α , utilizaremos a fórmula: α = 1 2 R C . Como os valores de R e C foram dados no enunciado, temos que:

α = 1 2 ( 32 ) ( 25 * 10 - 6 ) = 625   r a d / s

Já para ω 0 , temos que:

  ω 0 = 1 L C = 1 ( 160 * 10 - 3 ) ( 25 * 10 - 6 ) = 500

Portanto, comparando os dois valores, podemos afirmar que α 2 > ω 0 2 , portanto, o circuito é superamortecido, e a equação geral de v 0 ( t ) é:

v 0 t = A 1 e - s 1 t + A 2 e - s 2 t

Passo 3

Para calcular as raízes, faremos uso da seguinte fórmula:

s 1,2 = - α ± α 2 - ω 0 2

Com os valores de α e ω 0 encontrados no passo anterior, temos que:

s 1,2 = - 625 ± 625 2 - 5 00 2

s 1 = - 25 0 ;   s 2 = - 1 000

Com os valores das raízes, podemos colocar na fórmula do passo 2:

v t = A 1 e - 25 0 t + A 2 e - 1000 t

Passo 4

Para concluir a questão e determinarmos a expressão de v 0 t , encontraremos agora os valores de A 1 e A 2 .

Primeiramente faremos a seguinte relação:

v 0 0 = A 1 + A 2 =   100   V

Segundamente:

d v 0 d t 0 = - 250 A 1 - 1000 A 2 = 1 C - I 0 - V 0 R

- 250 A 1 - 1000 A 2 = 1 25 * 10 - 6 - 5 - 100 50 = - 325.000

Resolvendo as questões acima, temos que:

A 1 = - 300 ;   A 2 = 400

Portanto, podemos afirmar que:

v 0 t = - 3 00 t e - 25 0 t + 4 00 e - 10 00 t   V ,   t ≥ 0

Prontinho, pessoal!! Bora resolver mais uma questão juntos?

Resposta

v 0 t = - 300 t e - 250 t + 400 e - 1000 t   V ,   t ≥ 0

Exercícios de Livros Relacionados

As duas chaves no circuito visto na Figura P8.11 funcionam de modo sincronizado. Quando a chave 1 está na posição a , a chave 2 está na posição d . Quando a chave 1 passa para a posição b , a chave 2
A chave no circuito da Figura P8.14 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b . Determine v 0 ( t ) para t ≥ 0 .
O indutor no circuito da Figura P8.14 é aumentado para 125 mH. Determine v 0 ( t ) para t ≥ 0 .
Sabe-se que a resposta natural para o circuito mostrado na Figura 8.1 é v t =- 11 e - 100 t+20 e - 400 tV ,t ≥0 . Se C = 2 μ F e L = 12,5 H, determine i L ( 0 + ) em miliamperes.
A resistência do resistor no circuito do Exemplo 8.4 é alterada para 3.200 Ω . a) Determine a expressão numérica para v(t) quando t ≥ 0. b) Desenhe um gráfico de v(t) para o intervalo de tempo 0 ≤ t ≤