Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 35

Para o sistema mostrado abaixo, as tensões de linha são um conjunto equilibrado de sequência positiva com V a b = 300 ∠ 0 °   V (eficazes). Calcule a leitura dos medidores P A e P B e a potência total entregue à carga, se Z P = 10 ∠ 30 °   Ω .

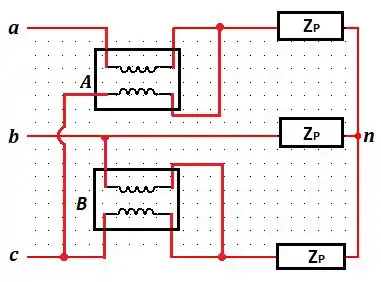
Passo 1

E vaaamos para mais uma de potência elétrica trifásica haha!!

Vamos começar primeiro encontrando as correntes de linha em a e b , ou seja:

I a = V a Z P = 300 3 ∠ - 30 ° 10 ∠ 30 ° = 30 3 ∠ 0 °   A

I b = V b Z P = 300 3 ∠ - 15 0 ° 10 ∠ 30 ° = 30 3 ∠ 18 0 °   A

Além disso, o enunciado nos fala da tensão de linha e da sequência a b c . O que ele quer que saibamos é:

V a b = 300 ∠ 0 ° V

V b c = 300 ∠ - 120 ° V

Passo 2

A leitura que o wattímetro A está lendo é dada por:

P A = V a b I a cos ⁡ θ V a b - θ I a ∴

P A = 300 × 30 3 cos ⁡ 0 - 0 ∴

P A = 3000 3   W

Ainda, a leitura que o wattímetro B está lendo é dada por:

P B = V c b I c cos ⁡ θ V c b - θ I c ∴

P B = 300 × 30 3 cos ⁡ - 12 0 - 18 0 ∴

P B = 1500 3   W

Logo, somando as duas potências, temos que a potência total fornecida às cargas é:

P = P A + P C = 4500 3   W

Simples né?! Bora para próxima ;)

Resposta

P A = 3000 3   W

P B = 1500 3   W

P = 4500 3   W

Exercícios de Livros Relacionados

A fonte trifásica equilibrada de sequência positiva na Figura P11.37 fornece 41,6 kVA,com um fator de potência atrasado de 0,707. A tensão de linha na fonte é 240 V.a) Determine o módulo da tensão de
A impedância Z no circuito trifásico equilibrado da Figura P11.19 é 100 - j75 Ω . Determine: I A B ,I B CeI C A . I a A ,I b BeI c C , I b a ,I c beI a c .
No circuito trifásico equilibrado da Figura P11.43, a bobina de corrente do wattímetroestá ligada à linha aA e a bobina de potencial do wattímetro está ligada às linhas b e c. Mostreque a leitura do w
Um gerador trifásico ligado em D tem uma impedância interna de 9 + j90 m Ω / ϕ . Quandoo gerador opera a vazio, o módulo de sua tensão terminal é 13.800 V. O gerador alimentauma carga ligada em ∆ por