Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 8

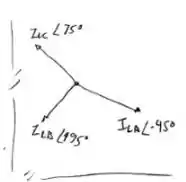
Um sistema equilibrado em Y-Y, trifásico e de sequência de fases positiva, tem V a n = 200 / 0 ∘ V (eficazes) e Z p = 3 + j 4 Ω . As linhas têm uma resistência de 1 Ω cada uma. Calcule a corrente de linha I L , a potência entregue à carga e a potência dissipada nas linhas.

Passo 1

Fala aí gurizada tudo certo? O enunciado pede que a gente determine a corrente de linha I L , a potência entregue à carga e a potência dissipada nas linhas.

V a = 200 ∠ 0 ∘ V

V b = 200 ∠ 120 ∘ V

V c = 2 ω ∠ 120 ∘ V

z p = 3 + 4 j

Passo 2

I B A = I f = V a 1 + Z p = 200 ∠ 0 ∘ 1 + 5 ∠ 53 , 13 ∘ = 25 - 25 j = 25 2 L - 45 ∘

I L B = 25 2 ∠ 195 ∘

I l c = 25 2 ∠ 75 ∘

V A Z = V a ⋅ Z p 1 + Z p = 200 ( 3 + 4 j ) 1 + 3 + 4 j = 175 + 25 j

P z p = P 1 ϕ = V A z ⋅ I A f c o s ⁡ θ v - θ i ⇒

P 2 p = 176,777 ⋅ 25 2 c o s ⁡ 0 ∘ + 45 ∘ = 4,42 k W

Passo 3

P 3 ϕ = 3 P 2 p = 13,26 k W

V R = V a - V A z = 200 - ( 175 + 25 j ) = 25 - 25 j = 25 2 ∠ - 45 ∘

P R = V R 2 1

Resposta

P R = V R 2 1

Exercícios de Livros Relacionados

Considere a Figura 12.51 e elabore um problema para ajudar outros estudantes a entender melhor os circuitos conectados em triângulo-triângulo equilibrado.
Determine as correntes I a , I b e I c no circuito trifásico da Figura 12.53 a seguir. Adote Z Δ =12–j 5Ω ,Z Y=4+j 6ΩeZ l = 2Ω .
No circuito da Figura 12.54, se V a b=440 ∠ 10 °,V b c = 440 ∠110 ° , V c a=440∠ 130 °V , determine as correntes de linha.
Uma fonte conectada em triângulo equilibrada tem tensão de fase V a b = 416 ∠ 30 °V e uma sequência de fases positiva. Se esta for conectada a uma carga em triângulo equilibrada, determine as corrente
As tensões linha-linha em uma carga conectada em estrela têm magnitude igual a 440V e estão na sequência positiva em 60H z . Se as cargas estiverem equilibradas com Z 1=Z 2=Z 3= 25 ∠30 ° , determine t