Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 5
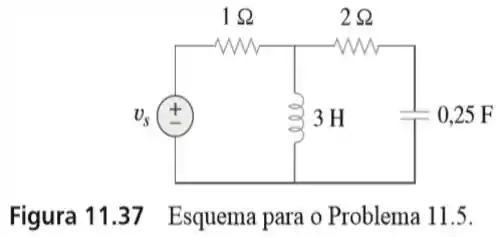
5. Suponha que no circuito da Figura , determine a potência média liberada para cada um dos elementos passivos. E determine a potência média absorvida por cada elemento.
Passo 1
Bom! O objetivo do problema é determinar a potência média liberada para cada um dos elementos passivos. E antes de mais nada, a primeira coisa importante para resolver essa questão, é saber que capacitores e indutores não absorvem potência. Sendo assim....
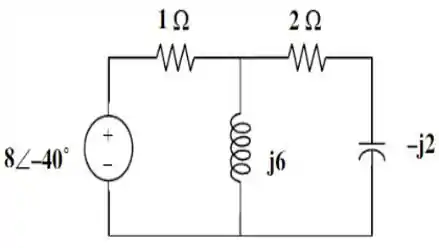
E a segunda coisa a fazer, é passar os elementos pro domínio da frequência:
nos resistores de e e comparar esse valor com o valor da potência complexa obtida para esse circuito.
E em seguida, bora fazer a análise nodal para esse circuito. Para isso, vamos redesenhá-lo mais uma vez, indicando as correntes, bem como nomeando os nós.
Aqui está...
Passo 2
Continuando nosso raciocínio, bora calcular a corrente circulando no resistor de . Ela é dada por...
Em seguida, temos que a potência média absorvida por esse resistor vale:
E por divisão de corrente, temos que a corrente circulando no resistor de vai valer:
De modo que a potência absorvida por esse resistor é igual a: