Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 2.Problemas - Ex. 25
A tensão no resistor de 16 V no circuito da Figura P2.25 é 80 V, positiva no terminal superior.
a) Determine a potência dissipada em cada resistor.
b) Determine a potência fornecida pela fonte ideal de tensão de 125 V.
c) Verifique que a potência fornecida é igual à potência total dissipada.
Passo 1
Iae, meus queridos! Td certinho??
Essa questão é bem bacana, que engloba potência e análise de malhas.
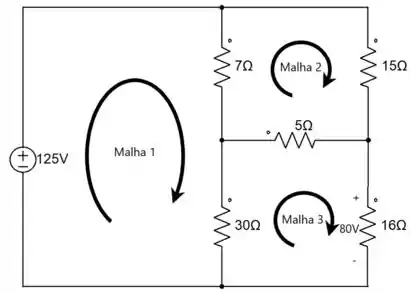
Temos 3 malhas no circuito, então teremos 3 equações de malhas
Malha 1
Malha 2
Malha 3
Organizando as equações, temos
Passo 2
Observando o circuito, vemos que é dado a partir do cálculo da lei de ohm no resistor de 16 ohms
Substituindo no sistema calculado acima, temos
Substituindo 1 ou 2 na equação 3, temos
E será
Na Letra a), vamos calcular a potência dissipada em cada resistor, pra isso, vamos analisar cada resistor, onde
No resistor de 7Ω, vemos que a corrente que passa por ele é dada por , logo
No resistor de 15Ω, a corrente que passa por ele é simplesmente , então
No resistor de 5Ω, a corrente é , logo
No resistor de 30Ω, a corrente é dada por
Por fim, no resistor de 16Ω, a corrente é simplesmente
Passo 3
Na Letra b), podemos calcular a potencia fornecida pela fonte, através da equação
Na letra c), para verificar que a potência fornecia é igual a potência dissipada, vamos verificar se
Ou seja
Iae, foi tranquilo? Bora praticar mais! 😎
Resposta
(a) ; ; ; ;
(b)
(c)