Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Questões para revisão - Ex. 1
A tensão no capacitor da Figura 10.43 é:
- b)
c) d)
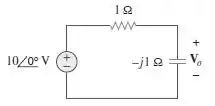
Passo 1
Vamos lá! Podemos resolver essa questão do mesmo modo que resolve em corrente contínua, mas para isso devemos levar o circuito para o domínio da frequência o que a questão já nos dispõe.
Portanto podemos fazer um divisor de tensão.
Passo 2
Lembre-se que:
Se resolvermos, temos:
Obs.: Caso sinta dificuldade de realizar operações com números complexos recomendo que assista nossas vídeo aulas sobre esse assunto!
Resposta
Item c)
Exercícios de Livros Relacionados
A frequência da fonte de tensão senoidal no circuito na Figura P9.39 é ajustada até que i g fique em fase com vg. a) Qual é o valor de v em radianos por segundo? b) Se vg = 15 cos vt V (onde v é a fre
A frequência da fonte de tensão senoidal no circuito da Figura P9.37 é ajustada até que a corrente i o fique em fase com vg. a) Determine a frequência em hertz. b) Determine a expressão de regime perm
Use o conceito da divisão de tensão para determinar a expressão de regime permanente para vo(t) no circuito da Figura P9.65, se vg = 120 cos 100.000t V.
O capacitor de 0,5 mF no circuito visto na Figura P9.69 é substituído por um capacitor variável. O capacitor é ajustado até que a tensão de saída esteja 135° adiantada em relação à tensão de entrada.
No circuito da Figura P9.63, suponha que va = 10 cos 16.000t V, vb = 20 cos 4.000t V. a) Qual é a técnica de análise de circuitos que deve ser utilizada para determinar a expressão de regime permanent