Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 9.Problemas - Ex. 68
No circuito da Figura P9.63, suponha que va = 10 cos 16.000t V, vb = 20 cos 4.000t V.
a) Qual é a técnica de análise de circuitos que deve ser utilizada para determinar a expressão de regime permanente para i o(t)?
b) Determine a expressão de regime permanente para i o(t).
Passo 1
Beleza pessoal?! Prontos para darmos início a mais uma atividade com o padrão de qualidade do responde ai?! Espero que sim pois vamos começar agora !!
- Para resolver este problema, usaremos o princípio da superposição. O princípio da superposição diz que se houver múltiplas tensões ou fontes de corrente em um circuito, isso é igual à soma dos múltiplos circuitos simplificados usando apenas uma das fontes.
- Aplicando o princípio da superposição explicado acima, dividiremos o problema em duas partes, pois temos duas fontes de tensão. Começando da esquerda para a direita, a parte esquerda do circuito com a fonte de tensão . nosso circuito fica assim
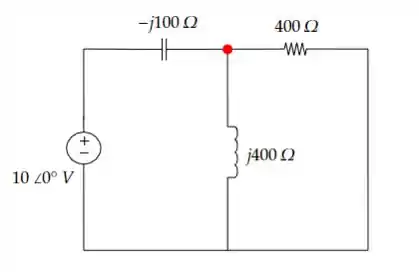
Da fonte de tensão dada nós sabemos que a frequência de saída é de A voltagem na forma polar é de A capacitância do condutor em forma polar é:
Agora, iremos calcular o valor da impedância do indutor,
Passo 2
Como temos componentes reativos (condutor e indutor) em nosso circuito, podemos fazer a análise nodal no ponto indicado pelo ponto vermelho na figura na quarta etapa. Podemos então calcular a tensão no nó como:
Agora iremos repetir o processo para o lado direito do circuito.
Da fonte de tensão , nós lemos que a frequência de saída é de 4000 rad/s. A tensão na forma polar é . A capacitância do condutor em forma polar é escrita:
Agora calculamos a impedância do indutor:
Passo 3
novamente, fazemos a análise nodal no ponto indicado com o ponto vermelho na figura acima. Podemos então calcular a tensão no nó como:
A tensão líquida em regime permanente é então a soma das duas tensões:
Resposta
- Veja a explicação!!!