Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 37
37. Um transformador elevador de tensão ideal de libera para uma carga resistiva. Calcule:
(a) A relação de espiras.
(b) A corrente no primário.
(c) A corrente no secundário.
Passo 1
Olha só! O enunciado nos disse que o transformador é elevador. Isso que dizer que ele recebe uma tensão menor e a transforma para uma tensão maior. Então, podemos desenhar o seguinte esquema...
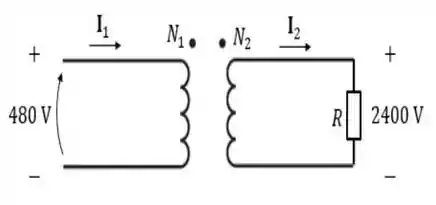
Onde a tensão do primário é:
E a do secundário é...
Como não foi dito nada sobre ângulo e a carga é resistiva, não precisamos nos preocupar com defasamentos. Por isso, vamos considerar apenas os módulos dos fasores.
Passo 2
a) Nessa letra, precisamos encontrar apenas a relação de espiras do transformador, ou seja...
Sabemos que a relação entre as tensões no primário e no secundário são diretamente proporcionais à relação das espiras em um transformador. Do jeito abaixo...
Logo, substituindo os valores das tensões no primário e no secundário, temos que:
Passo 3
b) Nessa letra, temos que calcular a corrente no primário. Para isso, vamos usar a fórmula da potência.
Como , temos que:
Passo 4
c) Pra terminar, temos que calcular a corrente no secundário . Sabemos que a relação entre as tensões mo primário e no secundário são diretamente proporcionais à relação de suas espiras enquanto a de corrente é inversamente. Sendo assim...
Então, conhecendo o valor de ...
Resposta
a)
b)
c)