Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 26

Uma fonte trifásica equilibrada, de sequência positiva, com V a b = 240 ∠ 0 °   V (eficazes), entrega 43.2   k W , com fator de potência unitário, a uma combinação em paralelo de uma carga conectada em Y com impedâncias de fase 4 + j 4   Ω e uma carga equilibrada conectada em Δ . Determine as impedâncias de fase da carga conectada em Δ .

Passo 1

Eaeeee!! Olha, se vc não conseguiu enxergar a forma em que as cargas estão conectadas, saiba que é da seguinte forma:

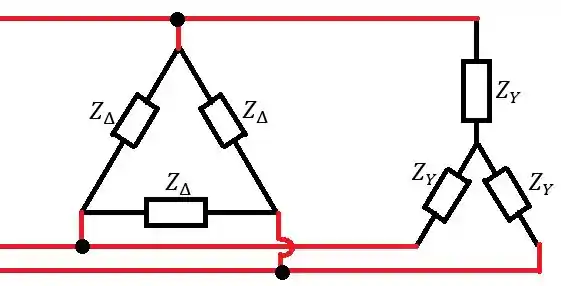
Para ficar mais simples, vamos chamar as cargas conectadas em Δ de Z Δ e as cargas conectadas em Y de Z Y .

Mas CUIDADO!! Calmaeee

Considerando a sequência positiva, tem uma defasagem entre as tensões de linha e as tensões de fase da seguinte forma:

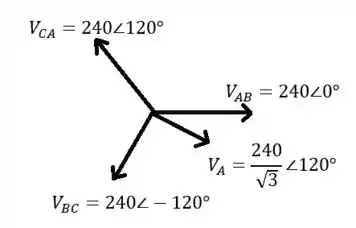
A questão também diz que o fator de potência é unitário, ou seja, a corrente e a tensão estão em fase!!

Passo 2

Vamos enxergar as cargas Z Δ em forma de Y . Pela seguinte relação, como as cargas são iguais, temos:

Z Y ' = Z Δ 3

Assim, temos:

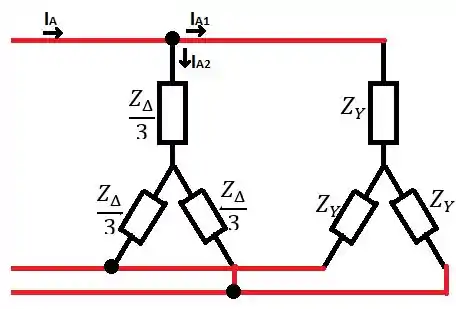
Passo 3

Pela figura anterior, temos:

I A 1 = V A Z Y = 240 ∠ - 30 ° 3 4 + j 4 = 10 6 ∠ - 7 5 °   A

Por outro lado, pela fórmula da potência trifásica (em valor eficaz), podemos descobrir I A , veja:

P 3 ∅ = 3 × V L × I L × F P ∴ I L = 43.2 ×   10 3 3 × 240 × 1 = 10 3.92 ∠ - 30 °   A

Obs: Colocamos ∠ - 30 ° por conta da diferença de fase entre I A e I L .

Logo, pela Lei dos nós (lembrando que I L = I A ), temos:

I A = I A 1 + I A 2 ∴

I A 2 = 104 ∠ - 30 ° - 24.5 ∠ - 75 ° ∴

I A 2 = 88.4 ∠ - 18.7 °   A

Passo 4

Dessa forma, temos que:

V A = Z Δ 3 × I A 2 ∴

Z Δ = 3 × 240 ∠ - 30 ° 3 88.4 ∠ - 18.7 ° = 4.61 - j 0.92   Ω  

Proooxima questão!!

Resposta

Z Δ = 4.61 - j 0.92   Ω

Exercícios de Livros Relacionados

Para um sistema trifásico equilibrado, se as tensões de fase são v a ( t ) = V m cos ⁡ ( ω t ) v b ( t ) = V m cos ⁡ ( ω t - 120 ° ) v c ( t ) = V m cos ⁡ ( ω t - 240 ° ) Então as correntes de fase sã
Demonstre (13.24).
No sistema da Fig. 13.20, as tensões de linha são um conjunto equilibrado, de sequência positiva, com V a b = 200 ∠ 0 °V (eficazes) e Z 1 = Z 2 = Z 3 = 10 ∠ 30 °Ω . Calcule a potência entregue à carga
Encontre as leituras dos wattímetros.
Calcule as leituras P A e P B dos wattímetros e a potência total entregue à carga se a fonte é equilibrada, conectada em Y , sequência a b c , com V a n = 100 ∠ 0 ° V (eficazes), e as impedâncias de f