Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 4.2 - Ex. 3
Usando a análise nodal, calcule V1, V2 e V3.
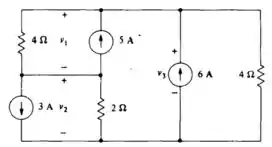
Passo 1
Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para achar as tensões e as correntes através da análise nodal. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??
A aplicação da LKC a um nó resulta em uma equação nodal, isto é, uma equação relacionando tensões de nós.
Ok, agora o nosso problema vai ser relembrar qual a relação entre a resistência e a condutância. Responde Aí!! Lembrou?? Não?!
Ela é
Passo 2
Para deixar de uma maneira mais clara, vamos enumerar esse circuito
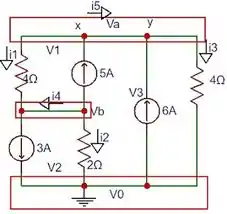
Agora já está bem mais fácil a visualização!!
Então vamos lá!!
A soma das correntes que deixam o nó tem que ser zero, e isto resulta na equação
Em termos das tensões de nó, esta equação fica
Aplicando a LKC ao nó , de maneira similar, obtemos
ou
Passo 3
Vamos para o passo final!!
Agora, como já temos todos os dados disponíveis, é só resolver a equação (1) e (2) por inspeção.
Fazendo equação (2) vezes 2 e mais a equação (1), chegamos em
Agora achando o que o enunciado pede
Como
Como
Como
Pronto!!
Resposta