Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 42

42. Reduza cada um dos circuitos na Figura 2 - 106 a um único resistor nos terminais a - b .

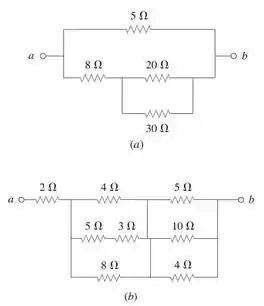
Passo 1

Bora lá resolver um probleminha sobre associação de resistores:

a) Vamos analisar esse primeiro caso:

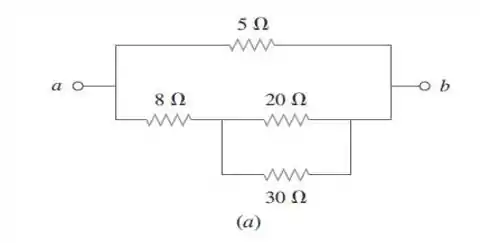
Vendo essa imagem, tiramos inicialmente que os resistores de 20   Ω e 30   Ω estão em paralelo. Calculemos a resistência equivalente para essa parte do circuito:

R e q 1 = ( 20 | | 30 )   Ω

R e q 1 = 20 ⋅ 30 20 + 30   Ω

R e q 1 = 12   Ω

Essa R e q 1 está em série com a resistência de 8   Ω . Só que elas duas estão em paralelo com a resistência de 5   Ω . Desse modo, a resistência total equivalente R a b   é dada por:

R a b = [ 5 | | 8 + 12 ]     Ω

R a b = 5 ⋅ ( 8 + 12 ) 5 + 8 + 12   Ω

R a b = 4   Ω

Passo 2

b) Vamos analisar agora, esse segundo caso:

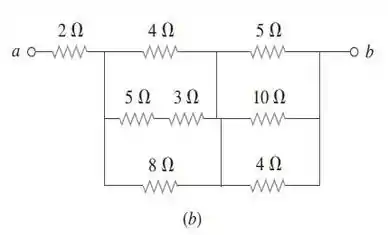
E em seguida, bora nomear com pontos cada um dos nós importantes desse circuito...

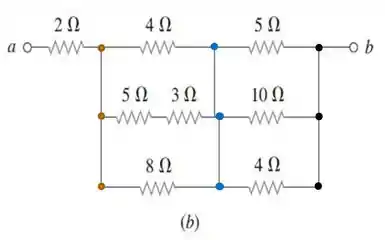
Os resistores de 5   Ω e 3   Ω estão em série. Assim, a resistência equivalente obviamente vai ser a soma 5 + 3 = 8   Ω .

E como podemos ver nos pontinhos que desenhamos, os resistores de 5 ,   10   e 4 Ω estão em paralelo. Todos eles estão entre um pontinho azul e um preto...

R e q 1 = ( 5 | | 10 | | 4 )     Ω

1 R e q 1 = 1 5 + 1 10 + 1 4 Ω

1 R e q 1 = 11 20 Ω

11 R e q 1 = 20

R e q 1 = 20 11   Ω

Seguindo nosso raciocínio, podemos ver também que as resistências de 4 ,   8   e 8 Ω estão em paralelo. A resistência equivalente R e q 2 , nesse caso, vale...

R e q 2 = ( 4 | | 8 | | 8 )     Ω

1 R e q 2 = 1 4 + 1 8 + 1 8 Ω

1 R e q 2 = 4 8 Ω

4 R e q 2 = 8

R e q 2 = 8 4   Ω

R e q 2 = 2   Ω

E para finalizar nosso raciocínio; basta observar que a resistência equivalente total R a b é dada pela associação em série de R e q 1 , R e q 2 e 2   Ω ...

R a b = 2 + 2 + 20 11   Ω

R a b = 5,818   Ω

Resposta

a)

R a b = 4   Ω

b)

R a b = 5,818   Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule v e a potência entregue pela fonte.
a) Mostre que a solução do circuito na Figura 3.9 (veja Exemplo 3.1) satisfaz a lei de correntes de Kirchhoff nas junções x e y.b) Mostre que a solução do circuito na Figura 3.9 satisfaz a lei das ten
Para cada um dos circuitos mostrados na Figura P3.4, a) determine a resistência equivalente vista pela fonte, b) determine a potência fornecida pela fonte
Determine a corrente e a potência fornecidas pela fonte de 40V no circuito do Exemplo 3.7 (Figura 3.32) substituindo o Δ inferior ( 25 ; 37,5e40Ω ) por seu Y equivalente.
Mostre que as expressões para condutâncias em Δ em função das três condutâncias em Y são G a = G 2 G 3 G 1 + G 2 + G 3 G b = G 1 G 3 G 1 + G 2 + G 3 G c = G 1 G 2 G 1 + G 2 + G 3 em que G a = 1 R a ,