Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 52
a) A chave no circuito da Figura P7.52 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b e permanece lá. Determine os valores inicial e final da tensão do capacitor, a constante de tempo para t $ 0 e a expressão para a tensão do capacitor para t $ 0. b) Agora, suponha que a chave no circuito da Figura P7.52 esteve na posição b por um longo tempo. Em t = 0, ela passa instantaneamente para a posição a e permanece lá. Determine os valores inicial e final da tensão do capacitor, a constante de tempo para t $ 0 e a expressão para a tensão do capacitor para t $ 0.
Passo 1
[a] – Para , o circuito tem a chave posicionada na parte a, então para uma corrente contínua, estável, o capacitor se torna um circuito aberto, logo, a configuração do circuito será da seguinte forma:
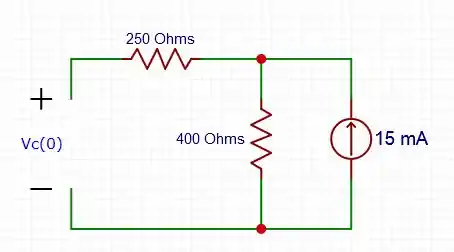
A tensão é a mesma da fonte de corrente, logo, fazendo-se uma conversão, temos:
Para , a chave muda para a posição b, logo, o circuito muda, ficando desse jeito aqui.
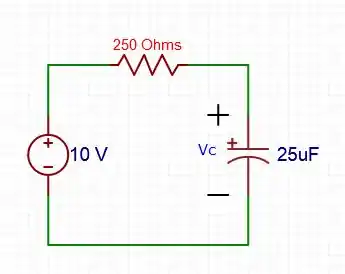
Com isso, temos as seguintes características:
Então, já podemos calcular a constante de tempo:
E usando a equação geral para a tensão, temos:
Substituindo os valores:
Passo 2
[b] – Agora, o problema pede inverter as ordens, em , a chave está posicionada em b, logo o circuito será desse jeito
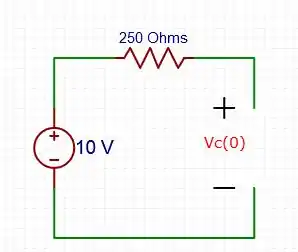
A tensão inicial é igual a .
Em , a chave está na posição a, logo o circuito muda:
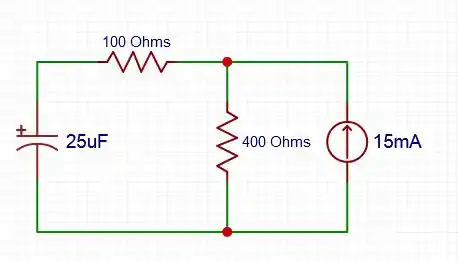
E a resistência equivalente:
Então:
Agora é usar a equação geral e partir para o abraço.