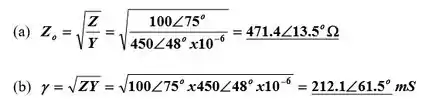Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas Abrangentes - Ex. 92
Uma linha de transmissão tem uma impedância em série igual a e uma admitância shunt de . Determine:
(a) a impedância característica
(b) a constante de propagação .
Passo 1
Então galera, calcular a impedância característica e a constate de propagação depende de apenas brincarmos com a impedância e a adimitancia shunt!
Passo 2
Não tem segredo galera, vamos cair pra cima de uma vez e jogar tudo na formula e computar os resultados! Vai dar bom!
Resposta
Exercícios de Livros Relacionados
Desenhe o diagrama de polos e zeros da função de rede do Ex. 14.5.1
Se a equação representativa de um circuito é d 2 v o d t 2 + 4 ⋅ d v o d t + 13 v o = 2 ⋅ d v i d t + 4 v i Calcule H(s) e os polos e zeros.
Se os zeros de H(s) são s = - 1 , - 1 ± j 1 , os pólos são s = - 2 , - 1 ± j 2 e H 0 = 4 , calcule (s).
Mostre que os parâmetros y podem ser obtidos a partir dos parâmetros z por onde Δ z = Z 11 Z 22 - Z 12 Z 21 . (Isso e dado na primeira coluna da segunda linha da Tabela 14.1.) Use esse resultado para
Calcule os parâmetros z e os parâmetros ABCD do circuito mostrado na figura abaixo.