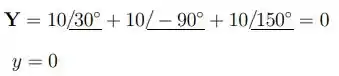Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 9.Problemas - Ex. 11
Use o conceito de fasor para combinar as seguintes funções senoidais em uma única expressão trigonométrica: a) y = 30 cos(200t - 160°) + 15 cos(200t + 70°), b) y = 90 sen(50t - 20°) + 60 cos(200t - 70°), c) y = 50 cos(5.000t - 60°) + 25 sen(5.000t + 110°) - 75 cos(5.000t - 30°) e d) y = 10 cos (vt + 30°) + 10 sen vt + 10 cos(vt + 150°).
Passo 1
Saaaalve galerinha. Tudo bem com vocês? Então bora lá. Começando no item a),
Passo 2
Aqui no item b), temos:
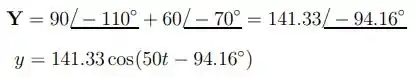
Item c),
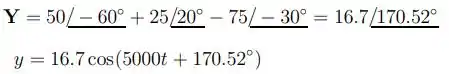
Passo 3
No item d),
Resposta
Exercícios de Livros Relacionados
Para o circuito do Ex. 14.3.2, tome i g 2 = e - 2 t c o s ( t + 45 ° ) A, permanecendo v g 1 como está, e calcule v por (a)usando superposição, (b) escrevendo uma única equação de nó e (c) usando tr
Calcule a resposta forçada i , se v_g = 4 e^(- t) cos t V .
Dada a função de rede H s = 4 s + 5 s 2 + 4 s + 5 E a entrada V i s = 2 ∠ 0 ° Calcule a resposta forçada v 0 ( t ) se (a) s = - 2 , (b) s = - 4 + j 1 e (c) s = - 2 + j 3 .
Das equações no domínio do tempo, calcule a resposta forçada v se v g = 10 j 8 t V . Usando o resultado em (a), calcule a resposta forçada v se v g = 10 cos 8 tV .
Calcule a representação fasorial de (a) 6 cos ( 2 t + 45 ° ) , (b) 4 cos 2 t + 3 sin 2 t , e (c) - 6 sin ( 5 t - 65 ° ) .