Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 49

Use o método das correntes de malha para determinar a potência total dissipada no circuito da Figura P4.49.

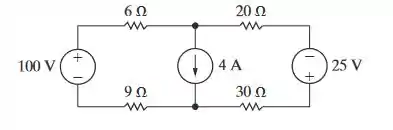
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Esse é um problema que envolve super malha, logo temos que fazer uma equação auxiliar para este caso, considerando a malha i 1 e i 2 , nós temos que

i 1 - i 2 = 4  

Agora, vamos aplicar o método das correntes de malha pela esquerda

- 100 + 6 i 1 - V 4 A + 9 i 1 = 0

Desenvolvendo

15 i 1 - V 4 A = 100   ( 1 )

Para a malha da direita, nós obtemos que

V 4 A + 20 i 2 - 25 + 30 i 2 = 0

Logo,

50 i 2 + V 4 A = 25   ( 2 )

Resolvendo o sistema, nós temos que

i 1 = 5   A

i 2 = 1   A

V 4 A = - 25   V

Passo 2

Agora, vamos calcular a potência dissipada pelos resistores, nós temos que

∑ P d i s s i p a d a = 6 i 1 2 + 9 i 1 2 + 30 i 2 2 + 20 i 2 2

Agora, vamos substituir os valores da seguinte forma

∑ P d i s s i p a d a = 15 5 2 + 50 1 = 425   W

Partindo para a fonte de tensão de 25   V , nós temos que

P 25 V = 25   V × - i 2

Com isso, nós temos que

P 25 V = 25 × - 1 = - 25   W

Está distribuindo potência, pelo fato do resultado ser negativo.

Passo 3

Calculando a potência desenvolvida pela fonte de corrente independente de 4 A

P 4 A = V 4 A × ( - 4 )

Substituindo os valores, nós temos que

P 4 A = - 25 × - 4 = 100   W

Está absorvendo potência, portanto, a potência total dissipada é igual a

∑ P d i s s i p a d a = P d i s s i p a d a r e s i s t o r e s + P 4 A

Substituindo os valores, nós obtemos que

∑ P d i s s i p a d a = 425 + 100 = 525   W

Resposta

P d i s s i p a d a = 525   W

Exercícios de Livros Relacionados

Resolva o Prob. 4.29 usando métodos da teoria de gráficos.
Calcule v no Ex. 4.3.1, se o elemento X é uma fonte de tensão dependente de 5i V com o terminal positivo na parte superior.
Usando análise de malhas, encontre i1 e i2 se o elemento x é uma fonte de tensão independente de 6 V, com o terminal positivo na parte superior.
Repita 0 Exerc. 4.5.1 com R1 = 1 Ω , R2 = 2 Ω , R3 = 4 Ω , vg1 = 21 V e vg2 = 0. Verifique os resultados empregando resistência equivalente e divisão de corrente.
Repita o Exerc. 4.5.3, se o elemento x é uma fonte de tensão dependente com 6i1 V, com o terminal positivo situado abaixo.