Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 63

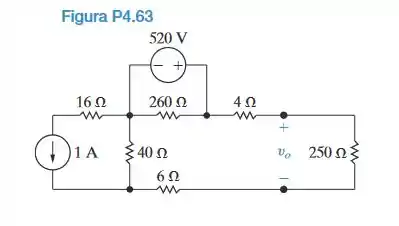
a) Use transformações de fonte para determinar v 0 no circuito da Figura P4.63.

b) Determine a potência gerada pela fonte de 520 V.

c) Determine a potência gerada pela fonte de corrente de 1 A.

d) Verifique que a potência total gerada é igual à potência total dissipada.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A – Vamos perceber algumas coisas, primeiramente, quando a fonte de corrente é conectada em série com um resistor, o resistor não afeta o circuito e pode ser substituído por um curto-circuito e quando a fonte de tensão é conectada em paralelo com um resistor, o resistor não afeta o circuito e pode ser substituído por um circuito aberto. Logo o circuito fica com a seguinte configuração

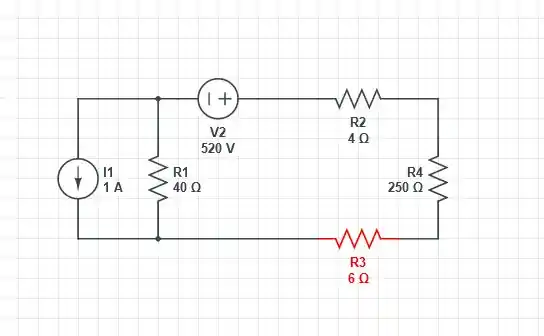
Agora vamos transformar a fonte de corrente em uma fonte de tensão, já que a mesma (a fonte de corrente, que isso fique bem claro!) está em paralelo com o resistor de 40   Ω , com isso, temos que

V = I R = 1 × 40 = 40   V

E o circuito fica

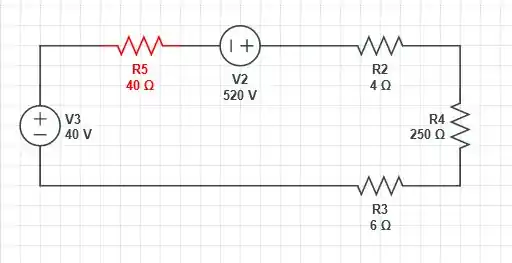
Passo 2

Dá uma tentação mexer com o resistor de 250   Ω , mas vamos deixar ele bem quieto, já que queremos descobrir a tensão nele, mas, os resistores 40   Ω ,   4   Ω   e   6   Ω estão em série, então vamos apenas somar as resistências

R e q = 4 + 6 + 40 = 50   Ω

As fontes também estão em série, logo, a fonte resultante é igual a

V r e s = 520 - 40 = 480   V

Logo, o circuito resultante é igual a

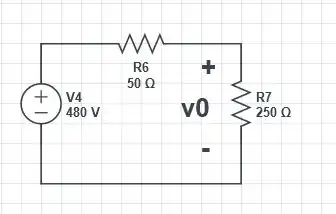
Passo 3

Já temos um belo circuito equivalente, com isso já podemos calcular v 0 , que será por divisor de tensão, então

v 0 = 480 × 250 50 + 250 = 400   V

A corrente I 0 pode ser calculada pela Lei de Ohm

I 0 = 400 250 = 1,6   A

Passo 4

B – A potência desenvolvida pela fonte de 520 V é igual a

P 520 V = V I = 520 × 1,6

Com isso, temos que

P 520 V = 832   W

Passo 5

C - A potência desenvolvida pela fonte de corrente é equivalente à potência desenvolvida pela fonte de tensão de 40 V, logo

P 1 A = P 40 V

Substituindo os valores, nós obtemos

P 1 A = V I = 40 × - 1,6 = - 64   W

A soma da potência desenvolvida é igual a

P d e s e n v o l v i d a = 832 - 64 = 768   W

Passo 6

D – A potência dissipada pode ser obtida da seguinte forma

P d i s s i p a d a = I 0 2 R e q

Onde R e q é a resistência equivalente e pode ser calculada, com isso

R e q = 250 + 50 = 300   Ω

Portanto,

P d i s s i p a d a = 1,6 2 × 300 = 768   W

Como característica interessante

P d e s e n v o l v i d a = P d i s s i p a d a = 768   W

Resposta

a )   v 0 = 400   V  

b )   P 520 V = 832   W  

c )   P 1 A = - 64   W

d )   P d e s e n v o l v i d a = P d i s s i p a d a = 768   W  

Exercícios de Livros Relacionados

a) Use transformações de fonte para determinar a corrente i o no circuito da Figura P4.61.b) Verifique sua solução usando o método das tensões de nó para determinar i 0 .
a) Use uma série de transformações de fonte para determinar i 0 no circuito da Figura P4.62.b) Verifique sua solução usando o método das correntes de malha para determinar i 0 .
a) Determine a corrente i o no circuito da Figura P4.60 fazendo uma série de transformações de fonte adequadas.b) Usando o resultado obtido em (a), faça os cálculos no sentido inverso para determinar
Duas fontes ideais de tensão cc são ligadas por condutores elétricos cuja resistência é r V/m, como mostra a Figura P4.102. Uma carga cuja resistência é R V move-se entre as duas fontes de tensão. Sen