Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 62

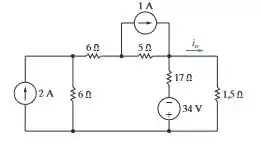
a) Use uma série de transformações de fonte para determinar i 0 no circuito da Figura P4.62.

b) Verifique sua solução usando o método das correntes de malha para determinar i 0 .

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Vamos aplicar a transformação de fontes para este caso, com isso, nós temos a seguinte configuração, a fonte de corrente de 2   A está conectada em paralelo com o resistor de 6   Ω será transformada em uma fonte de tensão de 12 V em série com o resistor de 6   Ω . A fonte de corrente de 1   A conectada em paralelo com o resistor de 5   Ω será transformada em uma fonte de tensão de 5   V em série com o resistor de 5   Ω . A fonte de tensão de 34 V conectada em série com o resistor de 17   Ω será transformada em uma fonte de corrente de 2 A em paralelo com o resistor de 17   Ω . O circuito resultante é igual a

A fonte de tensão de 12 V é conectada em série com a fonte de tensão de 5 V. Os dois resistores de 6   Ω são conectados em série com o resistor de 5   Ω , o circuito resultante é igual a

Podemos fazer uma transformação de fontes, a fonte de tensão de 17   V está conectada em série com o resistor de 17   Ω , podendo ser transformada em uma fonte de corrente de 1   A conectada em paralelo com um resistor de 17   Ω . Com isso, nós temos que

Passo 2

Esse circuito tem muitos pontos a ser observado, nós temos dois resistores de 17   Ω conectados em paralelo, então podemos substituir por um resistor equivalente, com isso

17 + 17 17 × 17 = 8,5   Ω

Uma coisa importante a notar é que temos duas fontes de corrente conectadas em paralelo. Então, usando o método da superposição, podemos substituí-los pela fonte de corrente equivalente 2 A - 1 A = 1 A, subtraímos os valores porque elas têm direções diferentes. O circuito é igual a

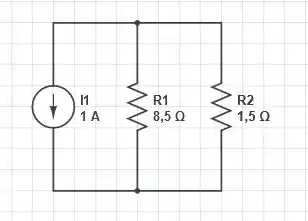
A corrente i 0 pode ser obtida usando um divisor de corrente, com isso

i 0 = - 1 × 8,5 1,5 + 8,5 = - 0,85   A

Logo

i 0 = - 850   m A

Passo 3

B – Aplicando o método das correntes de malha, na malha à direita, nós obtemos a seguinte configuração

17 + 17 I 1 + 17 I 1 - i 0 = 0

Simplificando

34 I 1 - 17 i 0 = - 17   ( 1 )

Na outra malha,

17 i 0 - I 1 + 1,25 i 0 = 0

Simplificando novamente

- 17 I 1 + 18,5 i 0 = 0

Resolvendo 1 e ( 2 ) , nós temos que

I 1 = - 925   m A   e   i 0 = - 850   m A

Logo,

i 0 = - 850   m A

Resposta

a )   i 0 = - 850   m A

b )   i 0 = - 850   m A

Exercícios de Livros Relacionados

Determine a potência total fornecida ao circuito da Figura P2.10, se v 0 = 5 V.
Determine a potência dissipada no resistor de 3k Ω do circuito da Figura P3.52.
Suponha que a fonte ideal de tensão da Figura 3.26 seja substituída por uma fonte ideal de corrente. Mostre que a Equação 3.33 ainda é válida.
O circuito de ponte mostrado na Figura 3.26 é alimentado por uma fonte de 24V cc. A ponte fica equilibrada quando R 1 = 500Ω , R 2 = 1.000Ω e R 3 = 750Ω .a) Qual é o valor de R x ?b) Qual é a corrente
a) Use uma série de transformações de fonte para determinar a tensão v 0 no circuito da Figura P4.59.b) Verifique sua solução usando o método das correntes de malha.