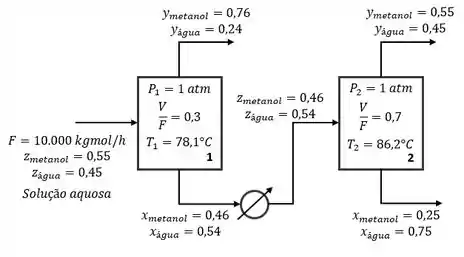
Dois tanques de flash são colocados conforme figura a seguir. A pressão de ambos é . A carga que entra no primeiro tanque é uma solução aquosa de metanol a molar. A vazão da carga é de . O segundo tanque opera com e a composição do líquido é de molar de metanol. Determine:
a) A fração vaporizada no primeiro tanque
b) , , , e .
Passo 1
Primeira coisinha que precisamos fazer em questões de flash é tentar entender a composição e informações de todas as correntes que temos.
Vamos preencher na própria figura da questão!
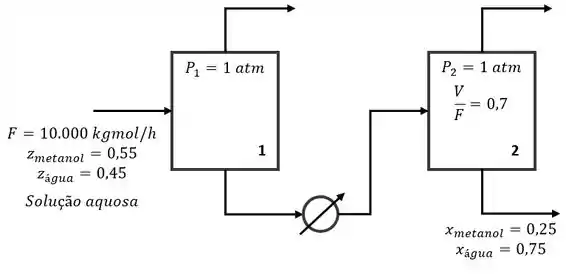
E precisamos determinar:
a) A fração vaporizada no primeiro tanque, ou seja,
b) , , , e , ou seja, a composição do vapor nos dois flashes, a composição do líquido no primeiro flash e a temperatura de operação desses caras.
Como conhecemos a saída do tanque 2 e o dele, vamos começar resolvendo tudo do tanque 2 e depois vamos para o tanque 1.
Passo 2
Nesse caso, nós vamos começar trabalhando com a corrente líquida de saída do segundo tanque. Vamos utilizar a corrente de saída, pois a partir dela vamos achar a temperatura do nosso segundo tanque!
Como a corrente de saída é líquida, podemos usar a simplificação para os casos onde . Então:
E nós sabemos como calcular em função das pressões parciais:
Então, substituindo na fórmula do flash simplificado:
E podemos obter através da Equação de Antoine:
Substituindo isso tudo na nossa equação de Flash simplificada para líquidos, obtemos que:
As constantes e da água e do metanolmsão tabeladas. O valor dessas constantes define a unidade da temperatura, a unidade da pressão e também se na equação de Antoine usamos ou . Então muita atenção para usar a equação adequada às suas constantes. Para a equação com , pressão em e temperatura em , temos os seguintes valores tabelados para as constantes:
E jogando elas na nossa fórmula e a composição dessa corrente de líquido, conseguimos achar a temperatura do tanque de flash 2 ().
Passo 3
Agora que já temos a temperatura, podemos calcular o para cada um dos nossos componentes.
E qual o nosso interesse no ? Ele tem mais uma forma de ser calculado, lembra?
Então através dele a gente consegue achar a especificação do vapor que tá saindo no topo da nossa coluna 2!
Até o momento, estamos com as seguintes informações então:
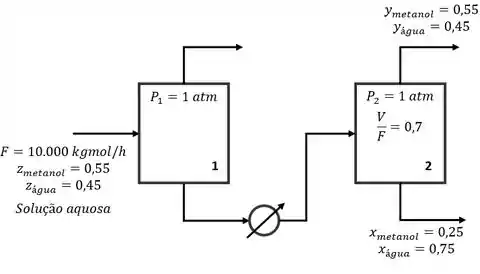
Passo 4
Então, a próxima coisa que precisamos calcular é a entrada do tanque 2 e para isso vamos utilizar a seguinte equação:
Sabendo que nosso é a mesma coisa que e foi dado na questão como , vamos substituit tudo aí na questão:
Portanto:
Logo:
Pois:
Então, temos agora todas essas correntes especificadas:
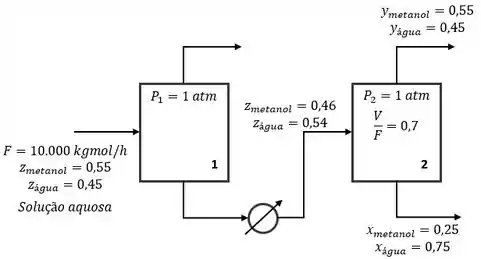
Passo 5
Vamos começar a falar sobre o tanque 1!
A saída do fundo (líquido) do tanque 1 é a entrada do tanque 2, que já especificamos, certo?
Portanto:
Então, como temos a composição do líquido especificada, podemos fazer o mesmo procedimento do tanque 2 (Passo 2) para calcular a temperatura do tanque 1.
Passo 6
Analogamente ao tanque 2 (Passo 3), vamos calcular os , já que já temos a temperatura, para depois conseguirmos achar os .
Utilizando novamente a definição de , temos como achar a composição do vapor que está saindo do tanque 1.
Passo 7
Última coisa que precisamos calcular nessa questão enorme é o do tanque 1. E, para calculá-lo, vamos recorrer a nossa equação de , já que temos todos os dados que precisamos!
Achando o .
E assim fica nosso esquema com todos os cálculos feitos. E essa é a nossa resposta final!
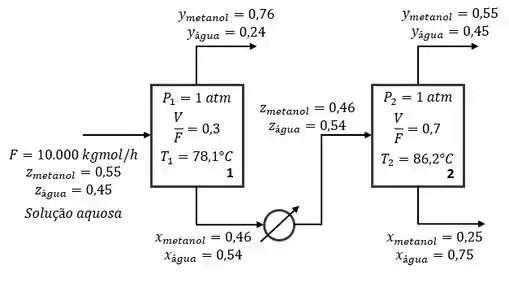
Resposta