Uma mistura binária é alimentada a um tambor de "flash" ("destilação integral") que opera no estado estacionário. A constante de equilíbrio de fases do composto A ( , na qual e representam, respectivamente, as frações molares do composto A nas fases vapor e líquida) é igual a 5 e a do composto B é igual a 0,5. O "flash" separa a mistura em duas correntes, uma líquida e outra vapor de igual vazão molar. A fração molar do composto A na corrente de alimentação ao "flash" é igual a:
a) 0,1
b) 0,2
c) 0,25
d) 0,333...
e) 0,666...
Passo 1
Vamos começar entendendo o que a questão pede para a gente calcular.
Nós precisamos determinar a fração molar de A na alimentação, em outras palavras, precisamos encontrar o .
Para isso, podemos tentar trabalhar com a nossa equação de Flash:
Sendo que os foram dados, mas ainda precisamos determinar o . Então é por aí que vamos começar!
Passo 2
Bem, se você leu essa questão e não encontrou o valor da porcentagem que foi vaporizada, relaxa! A questão não informa isso, mas deixa de uma forma beeem sutil um caminho para a gente calcular, beleza?
A questão diz que “o ‘flash’ separa a mistura em duas correntes, uma líquida e outra vapor de igual vazão molar”. Isso significa que o e , que saem do flash tem vazões molares iguais. Então, vamos dar uma olhada no equipamento de flash.
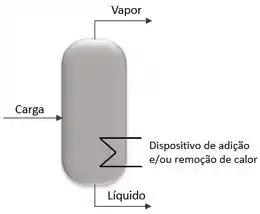
Se a gente fizer o balanço de massa, vamos ter:
Onde é a notação que usamos para carga. E como , obtemos que:
Para o , a gente sabe que ele é igual a:
Ou seja, nossa fração vaporizada! Nesse caso particular então:
Passo 3
Agora, vamos substituir os dados na nossa equação e ver o que falta!
Lembrando que e .
Porém, temos duas incógnitas ( e ). Então, como resolver isso!?
Bem, se só temos dois compostos na alimentação podemos dizer que a composição deles soma ! Portanto:
Logo:
Substituindo:
E resolvendo essa equação, obtemos que:
Assim, a resposta certa é a letra d!!!!
Resposta
Letra d)