A massa específica da água líquida é calculada por:
sendo a temperatura da água em . Se a temperatura se eleva em , qual é a elevação da espessura de uma lâmina de água de ? Considere que a água estava à temperatura ambiente antes do seu aquecimento.
Passo 1
O exercício quer saber a variação da altura do filme de água depois que ele aumenta de temperatura. Para facilitar nossa vida, podemos visualizar o problema de acordo com a imagem abaixo.
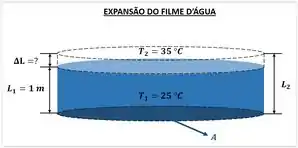
Ou seja, podemos considerar que o volume do filme de água aumenta sem aumentar a área da sua base. Em outras palavras, apenas a sua altura varia com essa expansão.
Para conectar as informações dadas, calculamos a variação relativa de volume do filme de duas formas e depois igualar os resultados encontrados pelos dois caminhos.
Pela primeira forma, nós vamos calcular geometricamente, considerando o volume igual à área da base do filme multiplicada pela sua altura.
onde:
- é a variação do volume de água;
- é o volume de água, quando ela está a ;
- é o volume de água, quando ela está a ;
- é a altura do filme de água, quando ela está a . O enunciado diz que ela vale ;
- é a altura do filme de água, quando ela está a ;
- é a variação da altura do filme de água. Essa é a incógnita do problema.
- é a área do filme de água.
A segunda forma de calcular a variação relativa de volume será o nosso próximo passo.
Passo 2
Pela segunda forma, vamos calcular termodinamicamente, considerando o volume como a divisão entre a massa da água e a sua massa específica. Temos que lembrar também que a massa de água não se altera durante sua expansão.
onde:
- , a massa específica da água, quando ela está a ;
- , a massa específica d aágua, quando ela está a ;
- , a massa de água.
Depois de igualar as duas equações de variação relativa de volume do filme e reorganizar a fórmula, encontramos uma expressão para a variação de altura .
As massas específicas são dadas indiretamente pelo enunciado a partir das equações:
onde:
- é a temperatura da água antes da sua expansão. Ela vale segundo o enunciado;
- é a temperatura da água depois da sua expansão. Ela vale segundo o enunciado.
Agora temos todas as informações necessárias para iniciarmos os cálculos, substituindo os dados.
Passo 3
Iniciamos os cálculos com a substituição dos valores de temperatura para achar as massas específicas:
Agora usamos os valores encontrados na fórmula da variação da altura do filme.