Escoamento sobre um Cilindro
Teoria
Introdução
Vamos nessa, meu time!
A ideia agora é a seguinte! Estamos interessados em calcular o coeficiente convectivo entre o fluido e um cilindro que é colocado de forma que o eixo do mesmo é perpendicular ao escoamento.
Se olharmos o cilindro de lado, teremos mais ou menos isso aqui:
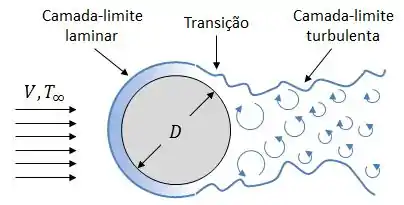
Agora, diferente do que vimos lá no caso da placa plana, nesse caso não vale a pena calcularmos o coeficiente local. Sendo assim, as correlações que veremos vão trabalhar apenas com o número de Nusselt médio e, consequentemente, com o coeficiente convectivo médio .
Vimos anteriormente que o número de Nusselt é geralmente uma função do número de Reynolds e do número de Prandtl . Bom, é um valor que depende do fluido. Já o número de Reynolds é dado por:
Também diferente do que vimos para placa plana, não vamos nos preocupar em determinar se o escoamento será laminar, ou turbulento, já que o escoamento através de um cilindro tende a apresentar essas duas fases de qualquer forma. ;)
Na real, os requisitos pra escolher as correlações que já já vamos ver, permite que possamos escolher duas ou mais correlações para um mesmo problema. Os resultados, no final das contas, vão ser bem próximos um do outro, então não precisa se preocupar tanto com qual correlação você vai escolher, desde que façamos isso direitinho. :)
Vamos ver, basicamente, três correlações.
Correlação de Hilpert
Vou te colocar de cara pro gol aqui, beleza?
Obs.: Não precisa se preocupar com o nome, ok? Coloquei aqui pra dividirmos isso direitinho.
A correlação é essa aqui:
Para essa correlação, as propriedades do fluido são avaliadas à temperatura de filme .
Essa fórmula é muito utilizada para , mas essa não é uma restrição.
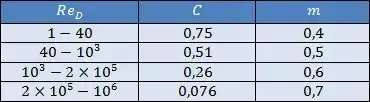
As constantes e para cilindros circulares são dadas pela tabela abaixo:
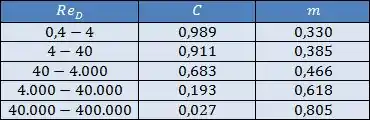
Para cilindros não-circulares, vem pra essa tabela aqui:
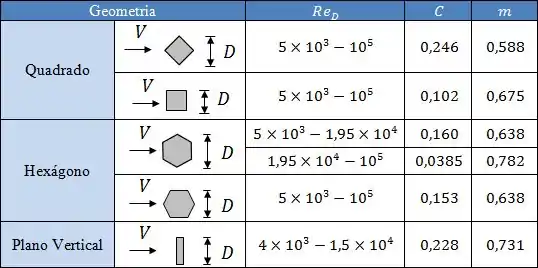
Correlação de Zukauskas
Sério, não se preocupe com os nomes, beleza? Hahahaha
Bom, essa correlação tem essa cara aqui:
Para essa correlação, as propriedades do fluido são avaliadas à temperatura de corrente livre .
Mas calma aí!
Tá vendo que temos ali um ... Esse número de Prandtl é avaliado na temperatura da superfície do cilindo (). Cuidado com isso, hein!
Essa correlação é válida desde que:
O coeficiente depende do valor do número de Prandtl . Se liga:
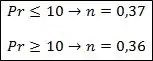
Pra fechar, os coeficientes e dependem exclusivamente do número de Reynolds , e são dados pela tabela abaixo:
Correlação de Churchill e Bernstein
Então, esses caras propuseram uma única equação que é válida para qualquer valor do número de Reynolds (#ousados) para o qual há dados disponíveis.
Essa equação é recomendada se e tem essa cara aqui:
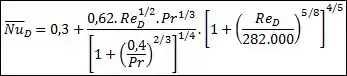
Para essa correlação, as propriedades do fluido também são avaliadas à temperatura de filme .
Novamente, não se preocupe com o quão feias são essas equações. O trabalho que teremos aqui é ver qual a correlação melhor se encaixa com os dados do problema e aplicá-la.
Pra facilitar, vamos matar as saudades do nosso passo-a-passo maroto.
Passo-a-passo diferenciado
Como o objetivo final quando trabalhamos com convecção é calcular justamente o coeficiente convectivo , vamos fazer o seguinte:
- Identifique a geometria do escoamento: Estamos trabalhando com um escoamento sobre uma placa plana, esfera ou cilindro?
- Identifique a temperatura de referência: Fique esperto se temos que usar a temperatura de filme ou a temperatura de corrente livre . Utilize essa temperatura pra pegar os dados sobre o fluido, incluindo o número de Prandtl.
- Calcule o número de Reynolds: Utilize o número de Reynolds pra determinar se o escoamento é laminar ou turbulento.
-
Escolha a correlação adequada a partir dos valores de e . Lembrando que:
- O coeficiente local é usado para determinar o fluxo em um ponto específico;
- O coeficiente médio é usado para determinar a taxa de transferência de calor em toda a superfície.
- Calcule o coeficiente convectivo .
- Seja feliz! :)
Vamos aplicar isso na prática?! ;)
Correlação de Hilpert
Correlação de Zukauskas
Correlação de Churchill e Bernstein
Passo-a-passo diferenciado
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Um tubo circular, com diâmetro externo de , é colocado em uma corrente de ar a e de pressão. O ar está em escoamento cruzado em relação ao tubo com uma velocidade de , enquanto a superfície externa do tubo é mantida a .
Qual é a taxa de transferência de calor saindo do tubo por unidade de comprimento?
Passo 1
Antes de qualquer coisa, precisamos definir as propriedades do fluido. Pra isso, usaremos como referência a temperatura de filme, dada por:
De acordo com a tabela A.4 do Incropera, temos o seguinte:
Agora podemos seguir em frente.
Passo 2
O próximo passo é calcular o número de Reynolds para que possamos decidir qual correlação usaremos:
Substituindo os valores:
Passo 3
O número de Nusselt médio tem essa cara aqui:
Para o valor do número de Reynolds que encontramos, temos que:
Logo:
Passo 4
O coeficiente convectivo médio será dado por:
Substituindo os valores:
Passo 5
Finalmente, a taxa de transferência de calor por unidade de comprimento será:
Substituindo os valores:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Para melhorar a dissipação térmica em um chip de silício, quadrado com , um pino de cobre é fundido à superfície do chip. O comprimento e o diâmetro do pino são e , respectivamente, e ar atmosférico a e está em escoamento cruzado em relação ao pino.
A superfície do chip, e portanto a base do pino, é mantida a uma temperatura de .
Supondo que o chip cause um efeito desprezível sobre o escoamento ao redor do pino, qual é o coeficiente convectivo médio na superfície do pino?
Desprezando a radiação e supondo que o coeficiente convectivo na extremidade do pino seja igual ao calculado na parta , determine a taxa de transferência de calor no pino.
Desprezando a radiação e supondo que o coeficiente de transferência de calor na superfície exposta do chip seja igual ao calculado na parte , determine a taxa total de transferência de calor saindo do chip.
Passo 1
Supondo que o chip cause um efeito desprezível sobre o escoamento ao redor do pino, qual é o coeficiente convectivo médio na superfície do pino?
Antes de qualquer coisa, precisamos saber as propriedades dos materiais que vamos precisar para resolver o problema.
Começando pelo ar e utilizando como referência a temperatura de filme, dada por:
A essa temperatura, de acordo com a tabela A.4:
Já para o cobre que está à temperatura de , de acordo com a tabela A.1, temos que:
Show! Agora já podemos seguir em frente!
Passo 2
O próximo passo é calcular o número de Reynolds, dado por:
Agora podemos partir para o número de Nusselt.
Passo 3
De acordo com a correlação de Hilpert, o número de Nusselt médio é dado por:
Para o valor do número de Reynolds que encontramos, temos que:
Logo:
Passo 4
O coeficiente convectivo médio será dado por:
Substituindo os valores:
Passo 5
Desprezando a radiação e supondo que o coeficiente convectivo na extremidade do pino seja igual ao calculado na parta , determine a taxa de transferência de calor no pino.
Para aletas com convecção na extremidade, a taxa de transferência de calor é dada por:
Onde:
Substituindo os valores:
Substituindo os valores de e na expressão de , teremos:
Ufa!
Passo 6
Desprezando a radiação e supondo que o coeficiente de transferência de calor na superfície exposta do chip seja igual ao calculado na parte , determine a taxa total de transferência de calor saindo do chip.
A taxa de transferência total de calor saindo do chip será dada por:
Onde representa a taxa de calor retirado do chip por convecção, dessa forma:
Onde:
Substituindo os valores:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um fio metálico fino com diâmetro está posicionado transversalmente a uma passagem para determinar a velocidade do escoamento a partir de características da transferência de calor.
Uma corrente elétrica é passada através do fio para aquecê-lo e o calor é dissipado por convecção para o fluido em escoamento. A resistência elétrica do fio é determinada por medidas elétricas e sua temperatura é conhecida a partir desta resistência.
Para um fluido com número de Prandtl arbitrário, desenvolva uma expressão para a sua velocidade em termos da diferença entre a temperatura do fio e a temperatura da corrente livre do fluido.
Qual é a velocidade de uma corrente de ar a e , se um fio com de diâmetro atinge uma temperatura de enquanto dissipa ?
Passo 1
Para um fluido com número de Prandtl arbitrário, desenvolva uma expressão para a sua velocidade em termos da diferença entre a temperatura do fio e a temperatura da corrente livre do fluido.
Vamos lá! Queremos uma expressão para a velocidade . A única expressão que temos visto que contém a velocidade é o número de Reynolds que, por sua vez, pode ser utilizado pra calcular o número de Nusselt médio . O número de Nusselt é utilizado pra calcular o coeficiente convectivo médio que, finalmente, é utilizado pra calcular a taxa de transferência de calor por unidade de comprimento (, já que o problema não nos disse nada sobre o comprimento do cilindro).
No final das contas, a ordem que temos que seguir pra encontrar uma expressão pra é:
A taxa de transferência de calor por unidade de comprimento é dada por:
Isolando o coeficiente convectivo, temos que:
Passo 2
O coeficiente convectivo médio está associado ao número de Nusselt por:
Logo:
O número de Nusselt possui a seguinte forma:
Substituindo a expressão do número de Nusselt e isolando o número de Reynolds:
Passo 3
Pra fechar a letra , o número de Reynolds é definido por:
Substituindo a expressão do número de Reynolds:
Passo 4
Qual é a velocidade de uma corrente de ar a e , se um fio com de diâmetro atinge uma temperatura de enquanto dissipa ?
Suponto , utilizando a equação de Zukauskas, temos , e .
Para as temperaturas dadas pelo problema, as propriedades do ar são dadas na tabela A.4 do Incropera para a temperatura de filme:
Logo:
Substituindo os valores:
Passo 5
Pra verificar se o nosso chute foi bom, vamos calcular o número de Reynolds pra a velocidade que encontramos pra ver se o mesmo está dentro da faixa que nós assumimos.
Como , a nossa suposição foi certa. :)
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Uma linha de alta tensão, com de diâmetro, possui uma resistência elétrica e está transmitindo uma corrente de .
Se ar ambiente a e , encontra-se em escoamento cruzado sobrea a linha, qual é a temperatura da sua superfície?
Passo 1
Antes de qualquer coisa, vamos encontrar as propriedades dos materiais que vamos necessitar pra resolver o problema.
Para o ar, vamos utilizar a tabela A.4 do Incropera, utilizando como referência a temperatura de filme, dada por:
“Opa! Como é justamente a temperatura na superfície que queremos calcular, como vamos fazer pra calcular a temperatura de filme?”
Nesse caso, a gente vai chutar um valor para a temperatura de filme e, no final das contas, vamos ver se esse chute foi bem dado. Como a temperatura ambiente é de , vamos chutar uma temperatura de filme .
Feito isso, temos que:
Passo 2
Calculando o balanço energia no sistema, temos que:
Logo:
Ambos os lados da igualdade possuem unidade de , onde é a resistência elétrica por unidade de comprimento (dada pelo problema).
Dessa forma, a temperatura na superfície será:
Dessa equação, o único termo que não temos é o coeficiente convectivo médio.
Então vamos trabalhar nesse cara.
Passo 3
O número de Reynolds é dado por:
Como começamos chutando alguns valores, para não correr o risco de usar uma correlação que não seja adequada, nós vamos utilizar a correlação de Churchill e Bernstein, que é a mais genérica.
Dessa forma:
Substituindo os valores de e , temos que:
Passo 4
O coeficiente convectivo médio será:
Agora que temos o coeficiente convectivo médio, basta substituí-lo na expressão que encontramos no Passo 2.
Resposta
Exercício Resolvido #5
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Componentes eletrônicos cilíndricos com de diâmetro e de comprimento e que geram calor a uma taxa de , montados sobre uma placa de circuito impresso, são resfriados com ar escoando sobre eles com uma velocidade de .
Se a temperatura do ar é de , determine a temperatura da superfície dos componentes.
Passo 1
A primeira coisa que temos que fazer aqui é determinar as propriedades do ar a . De acordo com a tabela A.4 do Incropera:
Agora podemos seguir em frente.
Passo 2
A temperatura superficial pode ser calculada através da seguinte expressão:
Onde . Para determinar por essa expressão precisamos do valor de , então vamos encontrá-lo!
Passo 3
O coeficiente convectivo é dado por:
Para calcular o número de Nusselt, precisamos do número de Reynolds, dado por:
Dessa forma, o número de Nusselt será dado por:
Para essa correlação, as propriedades do fluido devem ser dadas na temperatura de filme , mas como não conhecemos não podemos determiná-la, então vamos fazer os cálculos com a temperatura do fluido que foi dada e no fim, a gente confere se essa hipótese foi válida.
Substituindo então os valores:
Dessa forma, o coeficiente convectivo será:
Passo 4
Finalmente, a temperatura superficial será:
Passo 5
Agora que conhecemos podemos calcular a temperatura de filme e ver se usar ela nas contas afeta nossa resposta final:
Essa diferença de é muito pequena e afeta muito pouco nossa resposta final, escrevendo isso na questão, podemos considerar a encontrada como resposta final que tá tudo certo!
Mas pra mostrar pra você quão pouco afeta o valor final, eu refiz as contas com as propriedades à e encontrei os seguintes valores:
Como eu disse então, a gente usa o valor encontrado inicialmente e sinaliza que a diferença de temperatura nesse caso é desprezível.
Resposta
Exercício Resolvido #6
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Considere um tanque de água quente de de diâmetro e de comprimento. O reservatório é colocado sobre o telhado de uma casa. A água dentro do tanque é aquecida a por um coletor solar de uma placa plana durante o dia.
O reservatório é então exposto ao ar a com vento a uma velocidade média de durante a noite.
Estime a temperatura do reservatório durante um período de . Assuma que a superfície do tanque esteja na mesma temperatura que a água no interior e o coeficiente de transferência de calor nas superfícies superior e inferior seja o mesmo das superfícies laterais.
Passo 1
De acordo com valores tabelados, as propriedades da água a são dadas por:
Para as propriedades do ar, vamos utilizar a temperatura de filme, dada por:
A essa temperatura, de acordo com a tabela A.4 do Incropera, temos o seguinte:
Passo 2
A ideia aqui é a seguinte...
Podemos calcular a taxa de transferência de calor trocada nesses 45 minutos de duas formas. A primeira delas é calcular a quantidade de calor total trocada:
Onde é a temperatura final, e é a temperatura inicial do tanque. Logo em seguida, calcularíamos a taxa de transferência de calor dividindo o amigão acima pelo intervalo de tempo:
A segunda forma é utilizar a Lei de Resfriamento de Newton:
Se igualarmos essas duas expressões, podemos encontrar a temperatura final do tanque, onde a temperatura é dada pela média das temperaturas inicial e final do tanque:
Estamos calculando a temperatura superficial dessa forma justamente porque ela varia de a nos 45 minutos.
Igualando as duas expressões, teremos o seguinte:
Nessa expressão, o único cara que não temos é o coeficiente convectivo, então vamos atrás dele.
Passo 3
O coeficiente convectivo é dado por:
Pra calcular o número de Nusselt, precisamos do número de Prandtl (dado pelo problema) e do número de Reynolds, dado por:
Dessa forma, o número de Nusselt será dado por:
Substituindo os valores:
Dessa forma, o coeficiente convectivo será:
Passo 4
Voltando à expressão do Passo 2:
Onde:
Dessa forma, substituindo os valores:
Resposta
Exercício Resolvido #7
Questão 1, PUC, Lista 2
(Adaptado) Um anemômetro de fio quente feito de platina é operado no modo de temperatura constante para medir a velocidade de um escoamento de hélio. O diâmetro do fio é de 20 micrometros, seu comprimento é de e a temperatura de operação é .
Calcule a taxa de calor considerando uma corrente de hélio a e .
Passo 1
As propriedades do hélio devem ser obtidas à temperatura de filme, dada por:
De acordo com a tabela A.4 do Incropera, temos o seguinte:
Agora podemos seguir em frente.
Passo 2
O próximo passo é calcular o número de Reynolds, dado por:
Substituindo os valores:
Passo 3
Vamos calcular o número de Nusselt médio por:
Para o valor do número de Reynolds que encontramos, temos que:
Logo:
Passo 4
O coeficiente convectivo médio será dado por:
Substituindo os valores:
Passo 5
Finalmente, a taxa de transferência de calor por unidade de comprimento será:
Substituindo os valores:
Resposta
Exercício Resolvido #8
Questão 1, UFF, P2-2017.2
Suponha que você tenha uma escolha entre duas aletas pino. Uma possui uma área de seção reta quadrada com de lado e de altura e outra possui uma área de seção reta circular com de diâmetro e de altura.
Ambas são construídas de alumínio puro (propriedades à ). Em torno de cada aleta existe um ar circulando em velocidade de e temperatura de temperatura do meio é .
Assuma que o ar possui propriedades constantes e iguais a seu valor a 300 K. A base da aleta está a . Qual dessas terá a melhor relação (mais favorável em termos térmicos) de taxa de transferência de calor por peso de material para compor a aleta?
Despreze eventuais efeitos de convecção natural.
Passo 1
Antes de qualquer coisa, vamos pegar as propriedades do alumínio e do ar a . De acordo com a tabela A.4, para o ar:
Para o alumínio puro, de acordo com a tabela A.1:
Passo 2
A taxa de transferência de calor pode ser calculada da seguinte forma:
Assim, a primeira coisa que faremos será determinar o coeficiente convectivo para cada caso.
Passo 3
Para encontrar o coeficiente convectivo, precisamos do número de Reynolds, dado por:
Assim, para o pino circular:
Para o pino retangular:
Passo 4
O número de Nusselt será dado por
Para o pino circular, de acordo com o valor do número de Reynolds que encontramos, temos que:
Logo:
Para o pino retangular, como o valor que encontramos para o número de Reynolds está fora do intervalo tabelado, vamos usar a seguinte equação:
Passo 5
O coeficiente convectivo será:
Passo 6
Precisamos calcular agora o desempenho das aletas, para isso, vamos usar soluções tabeladas, onde, para a aleta circular:
Logo:
Para a aleta retangular:
Logo:
Passo 7
A taxa de transferência de calor para a aleta circular será:
Para a aleta retangular:
Passo 8
O peso da aleta circular será:
O peso da aleta retangular será:
Passo 9
A relação entre taxa de transferência de calor por peso de material para cada aleta será:
Aleta circular:
Aleta retangular:
Assim, a aleta retangular possui a melhor relação de taxa de transferência de calor por peso de material para compor a aleta.
Resposta
A aleta retangular possui a melhor relação de taxa de transferência de calor por peso de material para compor a aleta.