Escoamento sobre uma Esfera
Produzido por Giovanna RonzéTeoria
Sem mais delongas...
Então, meu time! Esse caso é muito semelhante ao escoamento sobre um cilindro, se liga:
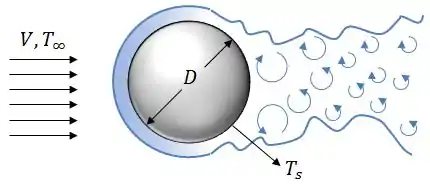
A diferença é que, agora, teremos somente uma correlação pra trabalhar. Ou seja, nem precisamos esquentar muito a cabeça pensando em qual correlação é a mais adequada pra resolver a nossa vida.

Assim como no caso do cilindro, não vale a pena aqui calcularmos o coeficiente local, então estaremos interessados somente no coeficiente convectivo médio . Dessa forma, vamos trabalhar somente com o número de Nusselt médio , dado por:
![]()
Onde o número de Reynolds é dado por:
![]()
Essa correlação é válida para:
Ou seja, basicamente ela abrange todos os casos em que veremos escoamentos sobre esferas.
Todas as propriedades do fluido são obtidas a partir da Temperatura de Corrente Livre , com exceção de , que é obtida a partir da Temperatura Superficial da Esfera .
Por enquanto, é isso! Mas antes de partirmos pros exercícios, vamos dar uma relembrada no nosso passo-a-passo.
Passo-a-passo diferenciado
O que queremos, no final das contas, é sempre calcular o coeficiente convectivo , certo? Bom, para isso, a boa é fazer o seguinte:
- Identifique a geometria do escoamento: Estamos trabalhando com um escoamento sobre uma placa plana, esfera ou cilindro?
- Identifique a temperatura de referência: No caso do escoamento sobre uma esfera, vamos usar como referência a temperatura de escoamento livre . A partir dessa temperatura, nós vamos pegar nas tabelas dos livros os dados sobre o fluido, incluindo o número de Prandtl.
- Calcule o número de Reynolds: No caso do escoamento sobre uma esfera, não vai fazer diferença se o escoamento é laminar ou turbulento, mas para muitos outros casos, isso faz diferença.
-
Escolha a correlação adequada a partir dos valores de e . Lembrando que:
- O coeficiente local é usado para determinar o fluxo em um ponto específico;
- O coeficiente médio é usado para determinar a taxa de transferência de calor em toda a superfície.
- Calcule o coeficiente convectivo.
- Seja feliz! :)
Vamos colocar isso em prática?! Responde Aí! ;)
Passo-a-passo diferenciado
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Ar atmosférico, a e a uma velocidade de , escoa em torno de um bulbo incandescente de cuja temperatura superficial é de .
O bulbo pode ser aproximado por uma esfera com de diâmetro. Qual é a taxa de transferência de calor perdida por convecção para o ar?
Passo 1
Vamos nessa, meu time!
A primeira coisa que temos que fazer é determinar as propriedades do fluido nas temperaturas de referência , para todas as propriedades, e para .
A , de acordo com a tabela A.4 do Incropera:
A , de acordo com a tabela A.4 do Incropera:
Passo 2
O próximo passo para calcularmos a taxa de transferência de calor é calcular o número de Nusselt, dado pela seguinte equação:
Onde:
Substituindo os valores:
Passo 3
Agora que encontramos o número de Nusselt, podemos calcular o coeficiente convectivo, se liga:
Substituindo os valores:
Passo 4
Finalmente, a taxa de transferência de calor será dada por:
Onde corresponde à área superficial da esfera. Dessa forma:
![]()
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Alterada) Um recipiente esférico de instrumentos para medições submarinas, usado para sondagens e para medir condições da água, tem um diâmetro de e dissipa .
Determine a temperatura superficial do recipiente quando suspenso em uma baia na qual a corrente de e a temperatura da água é de . Assuma para a água.
Inadvertidamente, o recipiente é retirado da água e suspenso no ar ambiente sem desativar a potência. Determine a temperatura superficial do recipiente com o ar a e uma velocidade do vento de . Assuma para o ar.
Passo 1
Antes de qualquer coisa, vamos pegar todas as propriedades que vamos precisar pra resolver o problema.
Todas as propriedades serão analisadas à temperatura de corrente livre , que é a nossa temperatura de referência.
A , de acordo com a tabela A.6 do Incropera para a água:
De acordo com a tabela A.4 do Incropera para o ar a :
Passo 2
Determine a temperatura superficial do recipiente quando suspenso em uma baia na qual a corrente de e a temperatura da água é de .
Agora que já sabemos os valores das propriedades, podemos calcular o número de Nusselt, dado por:
Onde:
Substituindo os valores, onde :
Passo 3
A taxa de transferência de calor será dada por:
Onde:
Logo:
![]()
Passo 4
Inadvertidamente, o recipiente é retirado da água e suspenso no ar ambiente sem desativar a potência. Determine a temperatura superficial do recipiente com o ar a e uma velocidade do vento de .
Novamente, começando pelo número de Nusselt, dado por:
Onde:
Substituindo os valores, onde :
Passo 5
Pra fechar, a taxa de transferência de calor será dada por:
Onde:
Logo:
![]()
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Revestimentos de alumínio altamente refletivos podem ser formados na superfície de um substrato pela aspersão da superfície com gotas de alumínio fundido.
As gotas são geradas em um injetor, deslocam-se através de um gás inerte (hélio) e devem ainda estar no estado líquido no instante da colisão.
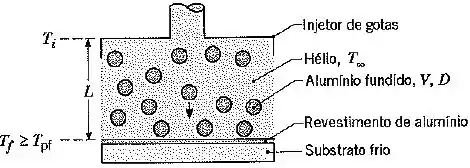
Considere condições nas quais as gotas com diâmetro, velocidade e temperatura inicial de , e , respectivamente, atravessam uma camada estagnada de hélio atmosférico que se encontra a uma temperatura de .
Qual é a espessura máxima permitida para a camada de hélio para garantir que a temperatura das gotas colidindo com o substrato seja maior que o ponto de fusão do alumínio ?
As propriedades do alumínio fundido podem ser aproximadas por , e .
Passo 1
Vamos entender o espírito da coisa, beleza?
Para calcularmos a espessura máxima da camada de hélio, precisamos saber o tempo necessário para as gotas de alumínio reduzirem a sua temperatura de a , já que:
Para calcularmos esse tempo, temos que resolver o problema de condução transiente nas gotas mas, para isso, precisamos do coeficiente convectivo médio.
Então, antes de mais nada, vamos levantar todas as propriedades (tanto do hélio, quanto do alumínio) que vamos precisar pra resolver o problema.
Vamos começar levantando as propriedades do hélio a . De acordo com a tabela A.4 do Incropera:
Para o hélio a (aproximadamente a média entre as temperaturas inicial e final), temos:
De acordo com o problema, temos que, para o alumínio:
Partiu resolver o problema de convecção.
Passo 2
Para encontrarmos o coeficiente convectivo médio, precisamos calcular o número de Nusselt, dado por:
Onde:
Substituindo os valores:
Passo 3
O coeficiente convectivo será dado por:
Show de bola! Agora podemos tratar da parte de condução transiente do problema.
Passo 4
Para resolver o problema de condução transiente, temos que ver se podemos usar o Método dos Parâmetros Concentrados, calculando o número de Biot, dado por:
Logo, o Método dos Parâmetros Concentrados vai resolver a nossa vida!
De acordo com o mesmo, o tempo necessário para o resfriamento é dado por:
Onde , e . Logo:
Substituindo os valores:
Passo 5
Finalmente, a espessura máxima da camada de hélio será:
![]()
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma junta de termopar esférica, com de diâmetro, é inserida no interior de uma câmara de combustão para medir a temperatura dos produtos de combustão. Os gases quentes possuem uma velocidade de .
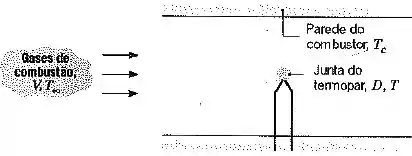
Se o termopar estiver a temperatura ambiente quando for inserido na câmara, estime o tempo necessário para que a diferença de temperaturas atinja da diferença de temperaturas inicial .
Despreze os efeitos da radiação e da condição através dos terminais do termopar. As propriedades da junta do termopar podem ser aproximadas por , e , e as dos gases de combustão por , e . Considere .
Passo 1
Para estimarmos o tempo para que a temperatura decaia, precisamos resolver um problema de condução transiente. No entanto pra resolver esse problema, precisamos calcular o coeficiente convectivo.
Para isso, precisamos começar calculando o número de Nusselt, dado por:
Onde:
Substituindo os valores:
Passo 2
O coeficiente convectivo médio é dado por:
Substituindo os valores:
Passo 3
Agora podemos tratar do problema de condução transiente. Então, logo de cara, vamos calcular o número de Biot pra saber se podemos usar o Método dos Parâmetros Concentrados:
Opa! Podemos usar o Método dos Parâmetro Concentrados sem peso na consciência. Assim o tempo necessário para o resfriamento será dado por:
Onde , e . Logo:
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma junta de termopar é inserida em um grande duto para medir a temperatura de gases quentes que escoam através do duto

Se a temperatura da superfície do duto for menor do que a temperatura do gás , o termopar irá medir uma temperatura menor, igual ou maior que a temperatura ? Justifique a sua resposta com base em uma análise simplificada.
Uma junta de termopar, na forma de uma esfera com de diâmetro e com emissividade superficial de , é colocada em uma corrente de gás que escoa a . Se o termopar mede uma temperatura de quando a temperatura superficial do duto é de , qual é a temperatura real do gás?
Pode-se considerar que o gás possua as propriedades do ar à pressão atmosférica.
Passo 1
Antes de mais nada, vamos determinar as propriedades do gás. Pra isso, vamos usar como como referência uma temperatura estimada em (sim, é um chute mesmo). Assim, de acordo com a tabela A.4 do Incropera para o ar:
Para a temperatura da superfície do termopar , temos que:
Beleza, agora podemos seguir adiante.
Passo 2
Se a temperatura da superfície do duto for menor do que a temperatura do gás , o termopar irá medir uma temperatura menor, igual ou maior que a temperatura ? Justifique a sua resposta com base em uma análise simplificada.
Bom, a taxa de transferência de calor por convecção do gás para o termopar deve ser igual à taxa de transferência de calor por radiação entre o termopar e a superfície do duto. Assim, podemos escrever que:
Se analisarmos a equação acima vemos que, se a temperatura do duto for menor que a temperatura do termopar , a temperatura do termopar deverá ser menor que a temperatura do gás .
Passo 3
Uma junta de termopar, na forma de uma esfera com de diâmetro e com emissividade superficial de , é colocada em uma corrente de gás que escoa a . Se o termopar mede uma temperatura de quando a temperatura superficial do duto é de , qual é a temperatura real do gás?
Opa! Podemos usar justamente a equação que encontramos no Passo 2 para calcular a temperatura do gás!
Dessa equação, nós temos quase tudo, com exceção do coeficiente convectivo médio. Então vamos atrás dele.
Passo 4
Pra calcular o coeficiente convectivo, precisamos calcular o número de Nusselt, dado por:
Onde:
Substituindo os valores:
Passo 5
O coeficiente convectivo médio será dado por:
Substituindo os valores:
Passo 6
Agora podemos finalmente calcular a temperatura do gás, se liga:
Substituindo os valores:
![]()
Resposta
A temperatura do termopar deverá ser menor que a temperatura do gás .
Exercício Resolvido #6
Questão 3, PUCRIO, P2-2003
Uma esfera de diâmetro igual a tem a sua superfície mantida a temperatura de . Ar escoa através da esfera a uma velocidade de e temperatura de . Calcule a taxa de transferência de calor entre a esfera e o ar.
Passo 1
Vamos começar determinando as propriedades do fluido nas temperaturas de referência , para todas as propriedades, e para .
A , de acordo com a tabela A.4 do Incropera:
A , de acordo com a tabela A.4 do Incropera:
Passo 2
O número de Nusselt, dado pela seguinte equação:
Onde:
Substituindo os valores:
Passo 3
Agora que encontramos o número de Nusselt, podemos calcular o coeficiente convectivo, se liga:
Substituindo os valores:
Passo 4
Finalmente, a taxa de transferência de calor será dada por:
Onde corresponde à área superficial da esfera. Dessa forma:
![]()
Resposta
Exercício Resolvido #7
Questão 1, PUCRIO, P1-2005
(Adaptado) Um esfera de aço de de diâmetro está inicialmente a temperatura uniforme e igual a . Ela é subitamente colocada em contato com o ar, que escoa com e com temperatura controlada e mantida igual a .
Calcule o coeficiente convectivo de troca de calor.
Passo 1
Vamos começar determinando as propriedades do fluido nas temperaturas de referência , para todas as propriedades, e para .
A , de acordo com a tabela A.4 do Incropera:
A , de acordo com a tabela A.4 do Incropera:
Passo 2
O número de Nusselt, dado pela seguinte equação:
Onde:
Substituindo os valores:
Passo 3
Agora que encontramos o número de Nusselt, podemos calcular o coeficiente convectivo, se liga:
Substituindo os valores:
Resposta
Exercício Resolvido #8
Questão 1, UFF, P2-2015.2
Considere uma esfera oca em que a temperatura da superfície interna é de e do ar exterior é de . No exterior, existe um escoamento que está a uma velocidade de .
Qual a temperatura da face externa do isolamento assumindo que o isolante possui 2 mm de espessura?
Considerar que a esfera oca seja feita de cobre com raio interno de e espessura de . Admita também que a condutividade térmica do material isolante seja constante e dada por . Assuma também que o cobre tem uma condutividade térmica constante e dada pelo seu valor a .
As propriedades termofísicas do ar são dadas pela tabela. Suponha nesse caso.
Passo 1
Pra calcular a temperatura da superfície externa de isolamento, podemos utilizar a expressão da taxa de transferência de calor entre o ar e a superfície externa do isolante:
Onde a taxa de transferência de calor pode ser calculada utilizando o conceito de resistência térmica. Como temos as temperaturas da superfície interna da esfera e do ar exterior:
Ainda assim, vamos precisar do coeficiente convectivo. Então a estratégia aqui será:
- Calculamos o coeficiente convectivo;
- Calculamos a taxa de transferência de calor;
- Calculamos a temperatura da superfície externa do isolante.
Passo 2
Antes de seguir em frente, precisamos determinar as propriedades do fluido nas temperaturas de referência , para todas as propriedades, e para .
A , de acordo com a tabela A.4 do Incropera:
Passo 3
Agora que já sabemos os valores das propriedades, podemos calcular o número de Nusselt, dado por:
Onde:
Substituindo os valores, onde :
Passo 4
A taxa de transferência de calor será:
Onde a condutividade térmica do cobre vale . Pra não ficar uma conta absurdamente grande, vou calcular cada resistência térmica separadamente. Logo:
Dessa forma:
Passo 5
Finalmente, a temperatura na superfície externa de isolamento será:
Substituindo os valores:
![]()